Factorization Machine笔记及Pytorch 实现

文章目录

1. 简介
2. 实现

简介

Factorization Machine(因子分解机)是Steffen Rendle在2010年提出的一种机器学习算法，可以用来做任意实数值向量的预测。对比SVM，基本的优势有：

• 非常适用与稀疏的数据，尤其在推荐系统中。
• 线性复杂度，在large scale数据里面效率高
• 适用于任何的实数向量的预测任务，包括:
  • 回归
  • 分类
  • 排序

目前推荐系统中，很多深度学习模型最后都会接一个FM来做评分的预测，或者情感分类等。网上关于FM的讲解资料很多，这里简单记录下。 首先FM的形式如下(后续黑体表示向量，普通字体为实数值)： \[y(\mathbf{x}) = w_0 + \sum_{i=0}^{n}w_ix_i + \sum_{i=1}^{n}\sum_{j=i+1}^{n}<\mathbf{v_i}, \mathbf{v_j}>x_ix_j\] 其中前两项为基本的线性回归，后面一项为向量的交互项，参数为：

• \(\mathbf{x} \in R^{n}\) 为一个输入的向量，维度为\(n\)
• \(\mathbf{w}\)为线性回归的参数
• \(\mathbf{V} \in R^{n \times k}\)为交互矩阵, k是factor 维度，属于超参数。 相对于为输入\(\mathbf{x}\)的每一个维度定义一个特征向量。
• \(<\mathbf{v}_i, \mathbf{v}_j> = \sum_{f=1}^k v_{i,f} \cdot v_{j,f}\) ，向量内积表示交互。

相比与SVM, 上述的模型完全是线性复杂度，并且由于对输入每个维度额外定义了一个因子向量\(\mathbf{v_i}\)，能够赋予更多的特征信息。 FM可以用于不同任务：

• 回归任务：直接以输出\(y\)作为回归值即可
• 分类任务：在\(y\)上接一个\(sigmoid\)，即：y = \(\frac{1}{1+e^{-y}}\)
• 排序任务: 将\(y\)作为输入\(x\)的score.

实现

如果直接按照公式来实现的话，第三项的复杂度为\(O(kn^2)\)，不过论文中通过因子变化，可以优化到\(O(kn)\)，具体推导如下，类似于\(2ab = (a+b)^2 - a^2 - b^2\)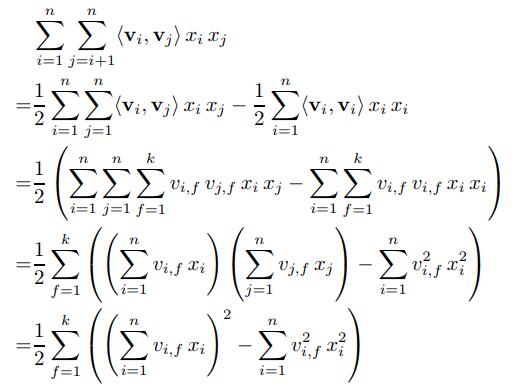： 这样复杂度即可降到\(O(kn)\), 转换为矩阵乘法即可。 pytorch的实现如下：

import torch
class FM_Layer(nn.Module):
    def __init__(self, n=10, k=5):
        super(FM_Layer, self).__init__()
        self.n = n
        self.k = k
        self.linear = nn.Linear(self.n, 1)   # 前两项线性层
        self.V = nn.Parameter(torch.randn(self.n, self.k))   # 交互矩阵
        nn.init.uniform_(self.v, -0.1, 0.1)
    def fm_layer(self, x):
        linear_part = self.linear(x)
        interaction_part_1 = torch.mm(x, self.V)
        interaction_part_1 = torch.pow(interaction_part_1, 2)
        interaction_part_2 = torch.mm(torch.pow(x, 2), torch.pow(self.V, 2))
        output = linear_part + 0.5 * torch.sum(interaction_part_2 - interaction_part_1, 1, keepdim=False)
        return output
    def forward(self, x):
        return self.fm_layer(x)

fm = FM_Layer(10, 5)
x = torch.randn(1, 10)
output = fm(x)

参考:

• Rendle S. Factorization machines[C]//Data Mining (ICDM), 2010 IEEE 10th International Conference on. IEEE, 2010: 995-1000.
• https://github.com/vanzytay/KDD2018_MPCN/blob/master/tylib/lib/compose_op.py