课程到此为止,一共介绍了PLA(感知机),Linear Regression(线性回归),Logistic Regression(逻辑回归)三种很相近的线性模型。这一节主要从error function分析介绍三种模型的联系,一些优化方法,最后如何延伸到多分类的情况。
线性模型回顾
首先PLA和Logistic Regression是分类模型,(严格来说, PLA是一个Algorithm而非Model,这里不作细分),而Linear Regression是一个回归模型,三者都是基于如下的线性方程进行建模的,这个方程也叫Linear Scoring Function(线性评分方程):\[\color{purple}{s}=w^Tx\]不同的是它们的hypothsis, 进而error function产生区别,如下图所示: 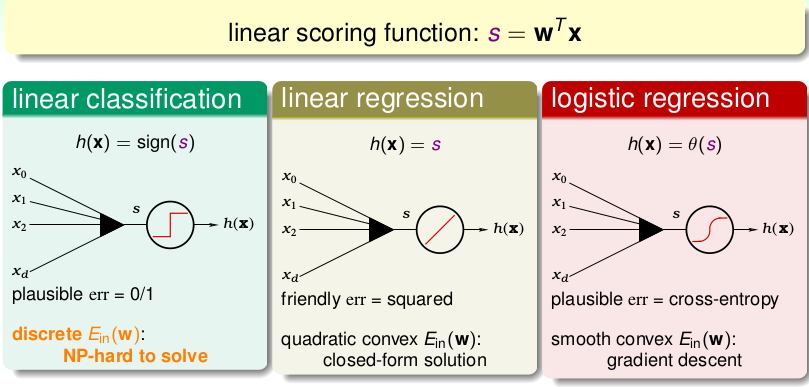
我们下面简单总结一下三者:
- PLA: 硬分类,直接输出+1 or -1,使用0/1损失函数,但是该损失函数是离散的函数,在优化的过程很难解(NP-HARD),也因此是使用另外的方式进行迭代求解。
- Linear Regression:回归,直接得到某个实数值,使用平方损失函数,得到连续二阶可微的凸函数,并且一阶微分为线性函数,可以直接求解最优参数,仅仅需要一次矩阵运算。
- Logistic Regression,软分类,输出某类的概率。使用对数损失函数也叫 cross error,得到连续二阶可微的凸函数,不过一阶微分函数非线性,很难直接求解,因此使用梯度下降的方式来迭代求解。
损失函数
可以看出,线性回归的求解相对来说,最简单,那我们能不能把它用到分类上呢?设置一个阈值,如果回归值大于阈值为+1, 小于为-1,就跟Logistic Regression一样,有个阈值即可。既然可以,那为什么不直接使用求解简单线性回归来分类呢?我们知道PLA的在线性可分的条件下,分类效果是最好的,那如果我们用其余两个做分类的时候,效果会怎么样呢?我们从它们三个的损失函数入手,为了统一形式,均构造为$\(ys\)的形式,如下图: 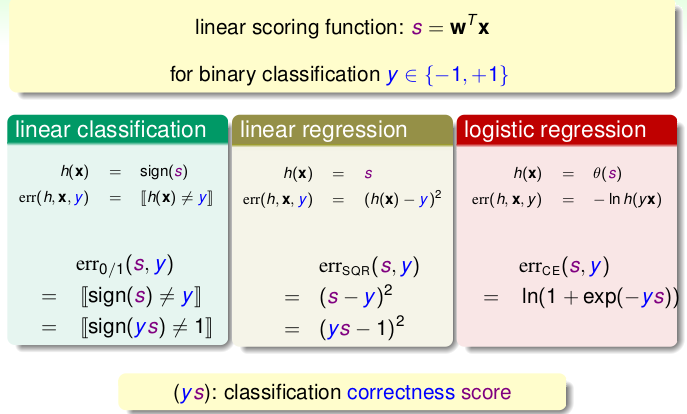
每个error-function里面都有\(ys\),我们可以考虑一下\(ys\)与\(err\)的大致关系:
- 0/1: 0 iff ys <0
- 平方: 当ys的绝对值比较大的时候, err也会很大。也有地方很接近与0/1损失函数
- cross-error: 相对平滑稳定很多,更加接近与0/1损失
我们作出函数图像看得更加直观,以ys为横坐标,err为纵坐标,如下:

我们已经知道了PLA的分类效果是最好的,因为只要线性可分的话,肯定可以把\(E_{in}\)降到最低,但是不容易优化!首先考虑Linear Regression,在图像上看到,当\(ys < 0\)时,\(err\)比较大,这个我们可以勉强接受,因为这时候PLA的分类也是错误的。但是当\(ys\)很大的时候,Linear Regression的\(err\)也很大,这种情况就不太理想了,因为此时PLA可以分类正确!接下来再看看Logistic Regression的损失函数整体趋势与PLA的0/1损失函数很接近,尤其在\(ys>0\)时。在\(ys<0\)的时候,\(err\)也比较大。
换句话说,\(err_{sqr}\)与\(err_{ce}\)可以作为\(err_{0/1}\)的upper bound。另外从图像中可以看出来,当\(err_{sqr}\)和\(err_{ce}\)比较小,即它俩分类效果比较好的时候,\(err_{0/1}\)同时也很小,这个很容易理解。
下面总结一下,对分类问题,PLA,Linear Regression,Logistic Regression三者的优缺点:
- PLA: 在线性可分的情况下,效果最好,可以有最小的\(E_{in}\); 缺点是: 必须是线性可分,否则需要用Pocket改进算法,这样的话,求解优势不明显。
- Linear Regression: 最优解求解最简单。缺点: 在\(|ys|\)比较大的时候,\(err\)这个bound太大。
- Logistic Regression: 求解相对简单。缺点: 在\(ys<0\)时, \(err\)偏大。
综上的话,在实际中做二分类的时候,经常先用Linear Regression 做一次,得到一个参数,将此参数作为Logistic Regression 或者 Pocket PLA的初始参数: \(w_0\),进而再去使用梯度迭代的方式最优化,这样可以很大程度上加速迭代的过程,更快得到最终解。 还有一点是,相对于Pocket PLA来说,在实际中用的更多的还是Logistic Regression。
SGD优化
前面说了,在实际中用的最多的还是Logistic 分类,但是我们也知道对应梯度\(\triangledown E_{in}(W)=\frac{\partial E_{in}(W)}{\partial W}=\frac{1}{N}\sum\limits_{n=1}^{N}\frac{1}{1+e^{y_nW^Tx_n}}(-y_nx_n)\),每次迭代都需要计算所有数据对梯度的贡献,这个在数据量很大的情况下,时间复杂度就很高了,因此这里就有了SGD(Stochastic Gradient Descent),也叫随机梯度下降的优化策略,即类似与PLA的标准算法,每次只选择一个数据点计算。在LR这里同样这样处理,每次只计算一个数据的梯度,这样经过多次迭代之后,与每次计算所有的数据的梯度效果很接近,但是时间复杂度很低,尤其是在数据量大的时候,或者 online-learning中应用最多。SGD的核心即修改更新方程如下:\[w_{t+1} \leftarrow w_t - \eta \frac{1}{1+e^{y_nW^Tx_n}}(-y_nx_n) \]当然它也有缺点,就是如果当前选择的点有噪音Nosie的话,可能不太稳定。
多分类问题
前面讲的都是二分类的问题,都是输出+1或者-1。但是在实际中,会经常遇到多分类的问题,这个时候只需要对前面的二分类算法PLA或者LR进行稍加修改即可。下面大致介绍两种利用二分类来解决多分类问题的方式。
OVA
OVA 即One Versus All,就是每次选中一个类别\(K\)作为圈圈,所有其它类别的作为叉叉,这样就构成了一个二分类的问题,然后我们用Logistic Regression得到一个模型,进而计算一下概率\(P_{K}\),同理一共构造\(N\)个分类器,然后选择概率最大的类别就可以了。
如下示意图,四个类别时候的情况:

这种方式很直观,有效。但是有缺点就是, 不平衡的问题,因为类别比较多而且很平均,这时候,每个类别的数据量远小于其它类别数据总量,这样的不平衡会导致算法不稳定。下面的OVO就是为了解决这个问题的。
OVO
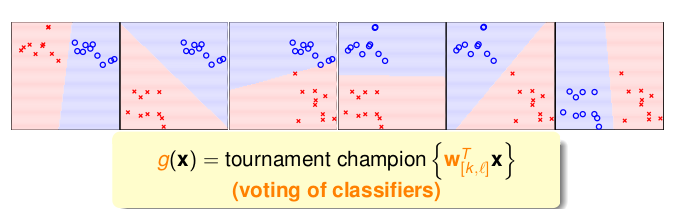
与OVA不同的是, OVO(One Versus One)每次只选出两个类别的数据进行分类,也就是说一共有\(\frac{n \times (n-1)}{2}\)个分类器,每个分类器会得到一种类别,然后我们只需要找出这\(\frac{n\times (n-1)}{2}\)中出现次数最多的,也就是被选中的最多的类别,作为最终的类别即可。
示意图如下,一共有四个类别,需要6个分类器,然后选出6个里面出现次数最多的类别,有点类似KNN算法。
总结
到这里,课程中的线性模型基本总结完了,在总结的过程中,参考了beader这系列博客的很多内容。林老师的讲解思路还是十分清晰的。接下来就是代码实现这几个简单的线性模型了。