11.27更新: logistic regression练习
前面一节介绍的是一个线性回归模型，不能直接用作分类问题。但是我们可以做一下修正，就可以达到分类的效果，其中逻辑回归(Logistic Regression)就是线性回归的一个延伸，专门用来做分类的模型，而且实际应用很广泛。
模型
模型方程
前面的PLA(感知机)是一个简单的二元分类模型，属于硬分类，即输出结果要么是+1,要么是-1。但是Logstic Regression是一个SOFT分类器，它计算的是某个数据属于某一类的概率，例:\(f(x) = P(+1|x)\)，这样\(P(-1|X)=1-P(+1|x)\)，我们选择概率大的作为我们的类别即可，但是我们知道线性模型的score的计算方法如下:\[s=\sum w_ix_i,\quad s \in R\]那我们如何把s转化为概率呢？也就是说找一个函数f使得: \(f: R->[0, 1]\), 还要保持原来的一些基本性质比如单调性等不变，这里面常用的一个[0,1]映射函数就是sigmoid函数\(\theta\): \[\theta(s)=\frac{e^s}{1+e^s}\]它的函数图像如下所示: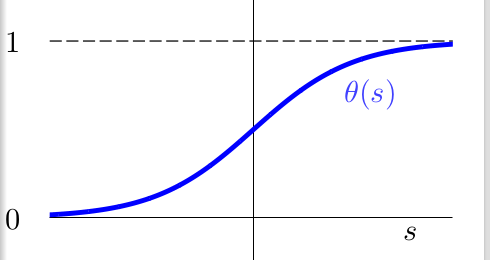 
现在我们就可以使用这样的输出在[0,1]的函数\(\theta(W^TX)=\frac{e^{W^TX}}{1+e^{W^TX}}=\frac{1}{1+e^{-W^TX}}\)，来作为我们的hypothesis。即我们的Logistic Regression方程就是:\[h(x)=P(+1|x)=\frac{1}{1+e^{-W^TX}}\]也就是数据x取+1的概率。
损失函数
下面就开始考虑如何求解模型参数，最关键就是定义损失函数\(E_{in}\)，不同于前面linear的平方损失，这里我们使用似然的思想来考虑，首先确定概率密度函数:\[h(x)=P(+1 | X) \Leftrightarrow P(y|x)= \left\{ \begin{matrix} h(x) & y=+1\\ 1-h(x) & y=-1\end{matrix} \right.\]另外需要注意的是，对于sigmoid函数\(h(X)=\theta(W^TX)\)时，有:\(1 - h(x) = h(-x)\)，因而整理为:\[P(y|x)=\left\{ \begin{matrix}h(x) & y=+1 \\ h(-x) & y=-1 \end{matrix} \right.=h(yx)\]这样我们就可以定义我们的似然函数了：\[L(W)=\prod\limits_{n=1}^{N}h(y_nx_n)=\prod\limits_{n=1}^{N}\theta(y_nW^Tx_n)=\prod\limits_{n=1}^{N}\frac{1}{1+e^{-y_nW^Tx_n}}\]然后求对数似然函数:\[l(W)=\sum\limits_{n=1}^{N}-ln(1+e^{-y_nW^Tx_n})\]我们需要最大化这个似然函数，但是我们知道的都是最小化的优化，我们可以直接求最小化负似然函数的\(W\), 也可以认为是我们的cost function, 如下:\[E_{in}(W)=\sum\limits_{n=1}^{N}ln(1+exp(-y_nW^Tx_n))\]
优化损失函数
我们通过对\(E_{in}(W)\)求二阶微分矩阵是正定矩阵(类似与一维中二阶导数大于0),可知\(E_{in}(W)\)是二阶连续，可微的凸函数，因此也可以梯度来求解。我们可以只需要求解一阶微分为0然后求解\(W\)即可，通过求一阶微分如下:\[\triangledown E_{in}(W)=\frac{\partial E_{in}(W)}{\partial W}=\frac{1}{N}\sum\limits_{n=1}^{N}\frac{1}{1+e^{y_nW^Tx_n}}(-y_nx_n)\]现在我们将求\(\min(E_{in})\)转为求解\(\triangledown E_{in}(W) = \textbf{0}\)，这里是向量0。然而跟Linear Regression直接解线性方程就能得到答案不一样的地方是，这是个非线性方程，很难去求解。因此让一阶微分为0去解\(W\)这条路走不下去了，那就只可以去迭代解了，就跟PLA的迭代求解一样，就是梯度下降(Gradient Descent)的方法来求最优解。我们知道梯度下降更新的方向是梯度的反方向，再考虑到更新布长，可以写出如下的梯度下降更新方程:\[\textbf{W}_{t+1}=\textbf{W}_t - \eta \triangledown E_{in}(\textbf{W})\]至于终止条件，最好的是\(\triangledown E_{in} = \textbf{0}\), 当然迭代到一定次数也可以。到这里，我们给出Logistic Regression 算法的一般过程:
- 初始化 \(\textbf{w}_0\)
- 对\(t=0,1,2...\),
- 计算\(\triangledown E_{in}(W)=\frac{\partial E_{in}(W)}{\partial W}=\frac{1}{N}\sum\limits_{n=1}^{N}\frac{1}{1+e^{y_nW^Tx_n}}(-y_nx_n)\)
- 更新: \(\textbf{W}_{t+1}=\textbf{W}_t - \eta \triangledown E_{in}(\textbf{W})\)
- 直到 \(\triangledown E_{in} = \textbf{0}\)或者到一定的迭代次数。
这里的\(\eta\)是学习速率，在实际中，根据经验一般取0.1效果比较好。学出了参数\(W\)，我们就可以用最优的hypothesis去给新数据分类了，即\(P(+1 | x_t) = \frac{1}{1+e^{-W^Tx_n}}\)，看看是否大于设定的阈值(大部分是0.5)即可。
总结
这一节主要讲了最基本的Logistic Regression的方程建立以及优化求解的过程，虽然带有回归两个字，但却是实实在在的分类算法。这一部分是最简单的逻辑回归，有很多地方可以优化。比如在梯度下降的部分每次需要计算所有训练数据对梯度的贡献值，与Pocket PLA 比较类似，复杂度稍高，可以用随机梯度下降的方式来优化，还有可以加正则项防止过拟合等等。另外这里只介绍了二分类的情况，下一节会在总结线性模型的基础上，介绍多分类的方法。