目前需要做Network Embedding方面的课题,而复杂网络本身就经常借鉴NLP的一些算法模型, Embedding也不例外. 因此先从Word Embedding入手。之前对Word Embedding(暂且翻译为词嵌入或者词向量)的理解就是将单词根据某种特征转为数值向量,再来做其他工作比如文本分类的工作。而word2vec则是word embedding的一种模型,也是目前使用最广的词向量模型, 由Google的Mikolov团队2013年提出。之前仅仅能够使用第三方库来训练直接使用, 对其中原理并没有多少理解, 这篇博客则比较完整的从背景知识到原理,参数训练等方面整理一下word2Vec。
Mikolov的两篇文章中涉及word2vec的细节甚少. 有不少人都对此模型作出了更加详细的解释, 本文主要沿着Rong, X.word2vec Parameter Learning Explained这篇文章的思路来整理一下,很多公式参考于这篇文章。
参考:
- Mikolov, T.(2013). Distributed Representations of Words and Phrases and their Compositionality.
- Mikolov, T.(2013). Efficient Estimation of Word Representations in Vector Space.
- Rong, X. (2014). word2vec Parameter Learning Explained.
背景
神经网络
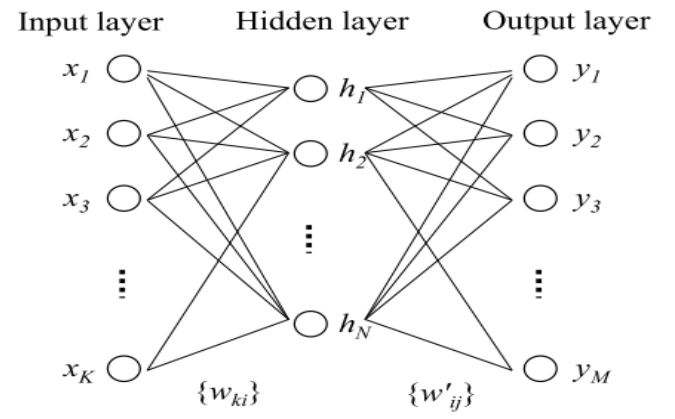
引入word2vec之前需要先对神经网络的知识有一定了解, 这里只贴一张图说明一个简单三层神经网络, 具体的细节不再赘述, 可以参考之前的一篇专门介绍神经网络的博文机器学习技法笔记(1)-神经网络 ; 如下图, \(x=[x_1, x_2,...x_K]\)是模型的输入, 中间经过与权重矩阵\(\{w_{ki}\}\) 运算, 矩阵运算结果再经过非线性激活函数得到隐层的结果\(h\), 从隐层到输出层同理. 这样从输入层到输出层既有线性变换,又有非线性变换, 因此可以更好刻画出输入变量的特征.
神经语言模型
作为Word Embedding的背景, 语言模型(Language Model)也是很有必要简要介绍一下.
统计语言模型就是用来计算一个句子的概率分布
简单来说,就是计算一个句子的概率, 语言模型用处很广泛,比如机器翻译中, 如何挑选一个概率尽可能大的句子也就是尽量靠谱的句子返回. 假设一个长度为\(m\)的句子,包含词:\([(w_1, w_2, w_3,..,w_m)\), 那么这个句子的概率,也就是这m个词共现的概率:
\[P(sen=(w_1, w_2, .., w_m)) = P(w_1)P(w_2|w_1)P(w_3|w_2,w_1)...P(w_m|w_{m-1}..w_1)\]
一般情况, 语言模型都是为了使得条件概率: \(P(w_t|w_1,w_2,..,w_{t-1})\)最大化, 不过考虑到近因效应, 当前词与距离它比较近的n个词更加相关(一般n不超过5),而非前面所有的词都有关, 因此上述公式可以近似为:
\[P(w_t|w_1,w_2,..,w_{t-1})=P(w_t|w_{t-1}, w_{t-2}...w_{t-(n+1)})\]
上述便是经典的n-gram模型的近似表示方式. 下面需要介绍一下神经语言模型(NNLM), 最初由Bengio提出的A Neural Probabilistic Language Mode最为经典, word2vec便是从其中简化训练而来. Bengio通过下面的一个三层神经网络来计算\(P(w_t|w_{t-1}, w_{t-2}...w_{t-n(+1)})\):
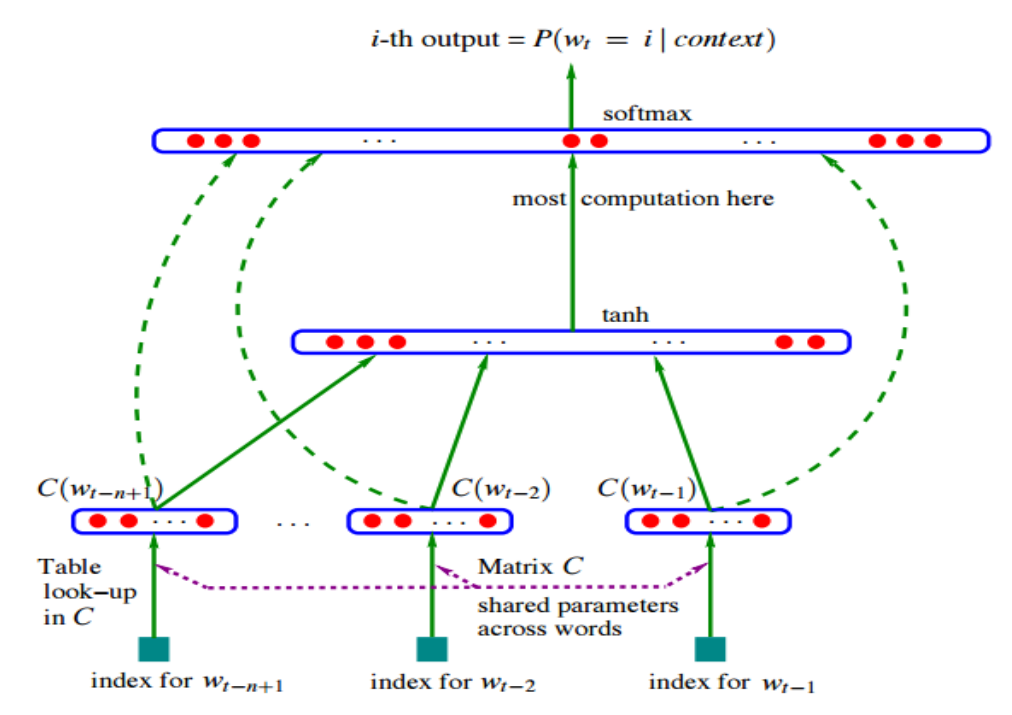
首先第一层输入就是前\(n-1\)个词\(w_{t-(n+1)},...,w_{t-1}\) 去预测第\(t\)个词是\(w_t\) 的概率. 这里面的矩阵\(C\in |V| \times d\)维护着词汇表中所有词的词向量, 其中\(|V|\)是词汇表中词的个数, \(d\)是词向量的维度. 然后根据输入的前\(n-1\)个词, 在C中找到它们对应的词向量, 然后直接串联起来成为一个维度为\((n-1)d\)的向量x 作为接下来三层神经网络的输入, 后面就是普通神经网络了. 需要说明的是,因为我们那要预测概率最大的\(w_t\), 因此最后输出层的神经元应该与词汇表大小同样为\(|V|\), 这里使用使用softmax函数归一化输出层的值到[0,1], 代表可能的每个词的概率. 此外在原文中, 存在一些直连边, 也就是上图中的虚线, 从输入层直接到输出层, 是一个线性变换, Bingo在文中表示, 直连边的存在大幅降低迭代次数, 但对语言模型效果无提升, 随着计算能力的提高, 后续的工作基本都去掉了直连边.
神经语言模型构建完成之后,就是训练参数了. 这里的参数包括词向量矩阵\(C\), 以及三层神经网络的权重, 偏置等参数. 训练数据就是大堆大堆的预料库. 训练结束之后, 语言模型得到了, 词向量也得到了. 换言之, 词向量是这个语言模型的副产品. 但是这个模型的缺点就是速度问题, 因为词汇表往往很大,几十万几百王, 训练起来就很耗时, Bengo仅仅训练5个epoch就花了3周, 这还是40个CPU并行训练的结果. 因此才会有了后续好多的优化工作, word2vec便是其中一个.
Word2Vec
简介
背景介绍完毕, 终于到主角了. word2vec是google于2013年的Distributed Representations ofWords and Phrases and their Compositionality 以及后续的Distributed Representations ofWords and Phrases and their Compositionality 两篇文章中提出的一种高效训练词向量的模型, 基本出发点是上下文相似的两个词,它们的词向量也应该相似, 比如香蕉和梨在句子中可能经常出现在相同的上下文中,因此这两个词的表示向量应该就比较相似.
word2vec模型中比较重要的概念是词汇的上下文, 说白了就是一个词周围的词, 比如\(w_t\)的范围为1的上下文就是\(w_{t-1}\)和\(w_{t+1}\). 在word2vec中提出两个模型(假设上下文窗口为3)
- CBOW(Continuous Bag-of-Word): 以上下文词汇预测当前词: \(w_{t-1}, w_{t+1}\) 去预测 \(w_t\)
- SkipGram: 以当前词预测其上下文词汇: \(w_t\) 去预测\(w_{t-1}, w_{t+1}\)
两个模型图示如下
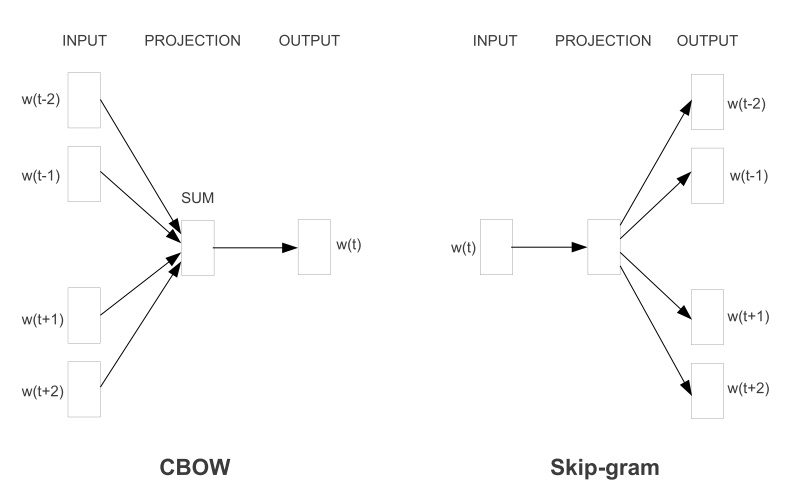
下面将会从最简单的上下文只有一个词的情形入手, 然后扩展到CBOW以及Skip-gram, 介绍原理以及参数训练过程. 关于word2vec的训练这里将会从完全的BP神经网络的过程来介绍.
One-Word Model
首先先看简化版入手: 输入输出都只有一个词, 如下图示:
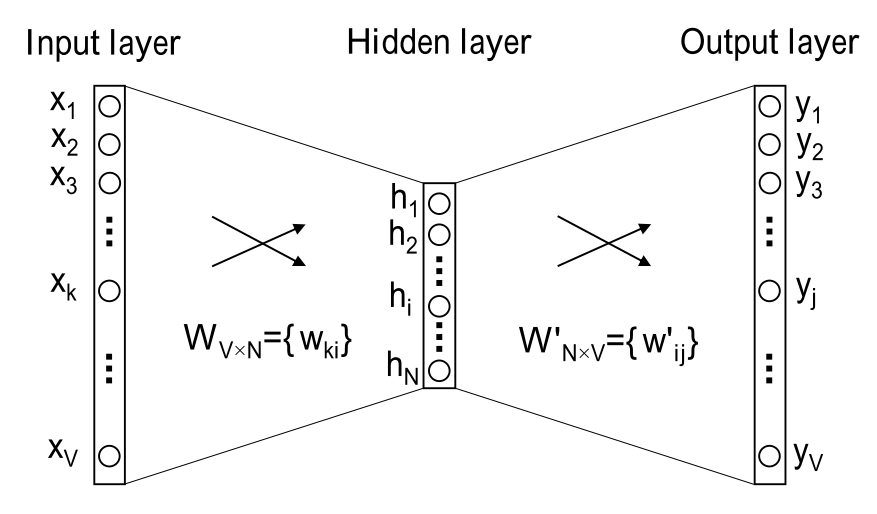
首先说明符号:
\(V\): 词汇表长度; \(N\): 隐层神经元个数, 同时也是词向量维度
\(W \in \mathcal{R}^{V\times N}\): 输入层到隐层的权重矩阵, 其实就是词向量矩阵,其中每一行代表一个词的词向量
\(W^{'} \in \mathcal{R}^{N\times V}\): 隐层到输出层的权重矩阵, 其中每一列也可以看作额外的一种词向量
下面从神经网络的前向过程开始介绍:
我们需要做的是用输入的词去预测输出的词. 其中 输入层的单词\(w_I\)使用one-hot来表示的, 即在上图中\(x_1, x_2, x_3,...,x_V\)只有\(x_k\)为1, 其余为0, 其中k可以是输入的词在词汇表中的索引下标. 之后就是经过词向量矩阵\(W\) 连接输入层和隐层. 其中由于X中只有一个1, 因此经过与W相乘, 相当于取出W中的的第k行,实际也就是输入单词的\(w_I\)的\(N\)维的词向量,使用\(v_{w_I}\)表示,来作为隐层的值,注意word2vec的隐层并没有激活函数:
\[\mathbf{h} = W^T \cdot X = v_{w_I}^T \]
然后考虑从隐层的\(\mathbf{h}\)到输出层\(Y\), 同样h经过矩阵\(W^{'}\)相乘,得到一个\(V \times 1\)的向量\(\mathbf{u}\):
\[\mathbf{u} = W^{'T} \cdot h\]
其中\(u\)每个元素\(u_j\) 就是\(W^{'}\)的第\(j\)列用\(v^{'}_{w_j}\)表示, 与\(h\)做内积得到: \(u_j = v_{w_O}^{'T}\cdot h\),含义就是词汇表中第\(j\)个词的分数,我们的目的就是要根据输入词\(w_I\)去预测输出的词,因此预测的词就取分数最高的即可,这里为了方便概率表示,使用softmax将\(\mathbf{u}\)归一化到[0,1]之间, 从而作为输出词的概率, 其实是一个多项分布, 也就是上图中的\(y\):
\[P(w_j|w_I) = y_j = \frac{\exp(u_j)}{\sum\limits_{k\in V} \exp(u_k)} = \frac{\exp(v_{w_j}^{'T}\cdot v_{w_I})}{\sum\limits_{k\in V} \exp(v_{w_k}^{'T}\cdot v_{w_I})}\]
其中\(v_{w}\)与\(v_{w}^{'}\) 都称为词\(w\)的词向量,一般使用前者作为词向量,而非后者,原因后续会解释。至此前向过程完成,就是给定一个词作为输入,来预测它的上下文词,还是比较简单的,属于简化版的神经语言模型。这个过程中需要用到的参数有两个词向量矩阵\(W, W^{'}\),下面就是重点了,介绍如何根据语料库来训练模型,更新参数,得到最终的词向量。
首先明确训练数据的格式,对于一个训练样本(\(w_I\), \(w_O\)),输入是词\(w_I\)的one-hot 的维度为\(V\)的向量\(\mathbf{x}\),模型预测的输出同样也是一个维度为\(V\)的向量\(\mathbf{y}\), 同时真实值\(w_O\)也是用one-hot表示,记为\(\mathbf{t}=[0,0,0,...1,0,0]\),其中假设\(t_{j^{*}} = 1\), 也就是说\(j^{*}\)是真实单词在词汇表中的下标,那么根据最大似然或者上面的语言模型,目标函数可以定义如下:
\[\begin{align*} O &= \max P(w_O|w_I) \\ & = \max y_{j^{*}} := \max \log y_{j^{*}} \\ &= \max \log(\frac{\exp(u_{j^{*}})}{\sum \exp(u_k)}) = \max u_{j^{*}}-\log\sum_{k=1}^{V}\exp( u_k) \end{align*}\]
一般我们习惯于最小化损失函数,因此定义损失函数:
\[E = -u_{j^{*}}+\log\sum_{k=1}^{V}\exp( u_k) \]
然后结合反向传播一层层求梯度,使用梯度下降来更新参数。
先求隐层到输出层的向量矩阵\(W^{'}\)的梯度:
\[\frac{\partial E}{ \partial w{'}_{ij}} = \frac{\partial E}{\partial u_j} \frac{\partial u_j}{\partial w^{'}_{ij}} = (y_j-t_j) h_i\]
这里面的\(y_j\)和\(t_j\)分别是预测和真实值的第j项,\(h_i\)是隐层的第\(i\)项。
考虑\(\frac{\partial E}{\partial u_j} = y_j - t_j\): 直接对原始求导,如下:
先考虑E的对数部分: \(\frac{\partial \log \sum\exp(u_k)}{\partial u_j} = \frac{\exp(u_j)}{\sum \exp(u_k)} = y_j\)
再看 \(-u_{j^{*}}\) 对 \(u_j\) 的梯度: 当\(j = j^{*}\)时,\(\frac{\partial -u_{j^{*}}}{\partial u_j}=-1 = -t_j\), 反之二者不等时,\(\frac{\partial -u_{j^{*}}}{\partial u_j}=0= -t_j\)
所以综合求导\(\frac{\partial E}{\partial u_j} = y_j - t_j\). 这个减法可以理解为输出层的第\(j\)项为预测值与真实值的差
因此梯度下降更新公式为:
\[w^{'}_{ij} = {w^{'}_{ij}}^{(old)} -\eta (y_j - t_j) h_i\]
整合为\(W^{'}\)的列向量\(\mathbf{v^{'}}_{w_j} = \{w^{'}_{ij}| i=1,2,3,...,N\}\)的形式如下:
\[\mathbf{v}^{'}_{w_j} = {\mathbf{v}^{'}_{w_j}}^{(old)} - \eta(y_j-t_j)\mathbf{h}, \ j \in \{ 1,2,3,...,V\}\]
也就是说对每个训练样本都需要做一次复杂度为\(V\)的操作去更新\(W^{'}\).
接着考虑隐层\(\mathbf{h}\)的更新,其实也是输入层到隐层的矩阵\(W\)的更新,继续反向传播,跟神经网络的相同, 输出层的\(V\)个神经元都会影响\(h_i\):
\[\frac{\partial E}{\partial h_i} = \sum_{j=1}^{V}\frac{\partial E}{\partial u_j} \frac{\partial u_j}{\partial h_i} = \sum_{j=1}^{V} (y_j-t_j)w^{'}_{ij} =W^{'}_{i} \cdot P\]
其中\(W^{'}_{i}\)是\(W^{'}\)的第i行, 这里为了方便书写, 令\(P = \{ y_j - t_j | j= 1,2,3,..,V\}\), 因此整合成整个隐层的向量\(\mathbf{h}\):
\[\frac{\partial E}{\partial \mathbf{h}} = W^{'} \cdot P\]
得到一个N维的向量,上面已经介绍过,\(\mathbf{h}\)就是词向量矩阵\(\mathbf{W}\)的一行: $ = W^T X = v_{w_I}^T \(, 但是因为X中只有一个1,因此每次只能更新\)\(的一行\)v_{w_I}\(,其余行的梯度\) = 0\(, 所以\)v_{w_I}$的更新公式为:
\[v_{w_I}^T = v_{w_I}^T - \eta W^{'} \cdot P\]
到此为止, 一个训练样本的反向传播训练过程就为止了。 我们可以看到,对于输入层到隐层的矩阵\(W\) 我们每次训练只需要更新一行向量即可,而对于隐层到输出层的矩阵\(W^{'}\)的所有\(N \times V\)个元素都需要更新一遍,这里的计算量还是很大的。
这一节主要比较细致的介绍了最简单的输入输出只有一个单词的情况的推理和训练的过程,后面的CBOW(上下文预测单词)以及SG(单词预测上下文)均基于这一节扩展开来。
CBOW Model
这一部分讲word2vec的第一个形式: Continurous Bag-Of-Word,模型图示如下:

跟上一个模型唯一的不同就是输入不再是一个词\(w_I\), 而是多个词,上图中一共有C个单词: \(x_{1k},x_{2k},...,x_{Ck}\),每个\(x\)都是one-hot表示。 这样隐层的\(\mathbf{h}\)的计算就会不同了: 之前一个单词的模型是直接取出\(W\)的一行\(v_{w_I}\)作为\(h\)的值,在CBOW中则是取出\(W\)中输入的所有C个单词的词向量,然后直接取平均,如下:
\[\begin{align*} \mathbf{h} &= \frac{1}{C} W^T(x_{1} +x_2+...+x_{C}) \\ &= \frac{1}{C}(v_{w_1} + v_{w_2}+...+v_{w_C})^T\end{align*}\]
后面隐层到输出层的过程与One-Word Model 一模一样,包括目标函数定义, 反向传播训练等。将\(W^{'}\)的更新公式照抄下来如下,依旧是每次都需要更新所有的行:
\[\mathbf{v}^{'}_{w_j} = {\mathbf{v}^{'}_{w_j}}^{(old)} - \eta(y_j-t_j)\mathbf{h}, \ j \in \{ 1,2,3,...,V\}\]
隐层神经元的梯度也相同:
\[\frac{\partial E}{\partial \mathbf{h}} = W^{'} \cdot P\]
下面考虑输入层到隐层稍微有些不同,在One-Word Model里面因为输入只有一个词,因此每次训练只更新这个词对应到\(W\)的那一行,但是在CBOW里面有多个词,这里采取的策略是将\(\mathbf{h}\)的梯度均摊到每个词上,因此每次训练会更新\(W\)中的C行,如下:
\[v_{w_{I,c}}^T = v_{w_{I,c}}^T - \frac{1}{C}\ \eta W^{'} \cdot P,\ \ c=1,2,...,C\]
到此为止 CBOW 的推理和训练过程也介绍完毕,基本跟One-Word Model 一样。
SkipGram Model
现在开始介绍word2vec的第二种形式: SkipGram(根据单词预测上下文),这个模型与One-Word Model不同的地方在于,SG的输出有多个词,而非One-Word 中输出只有一个词,这样输出层就不是一个多项分布了,而是\(C\)个多项分布了,模型图示如下:
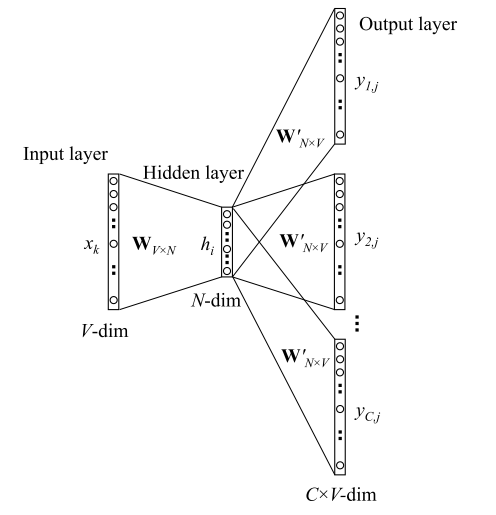
因此从输入层到隐层部分与One-Word Model 相同,隐层神经元的计算方式如下:
\[\mathbf{h} = W^T \cdot X = v_{w_I}^T \]
因为输出层是有C个单词, 因此有C个多项分布: \(y_{1}, y_{2}...y_{C}\), 因此前向计算的过程也需要分开计算,如下公式,用来计算第\(c\)个输出单词的预测的多项分布中第j项,相比One-Word Model 多了一个c参数:
\[P(w_{c,j}|w_I) = y_{c,j} = \frac{\exp (u_{c,j})}{\sum_{k=1}^{V} \exp(u_{c,k})}\]
需要主要的是这\(C\)个输出向量是相互独立的,可以当做是独立的\(C\)个One-Word Model 中的输出向量,相互之间没有影响,并且从图中也可以看出,连接隐层与C个输出层的参数矩阵\(W^{'}\)是共享的,于是便有: \(u_{c,j} = u_{j} ={v^{'}_{w_j}}^T \cdot \mathbf{h}\) 这里的\(v^{'}_{w_j}\)的含义与One Word Model 中相同,都代表\(W^{'}\)的第j列,同时也是词汇表中第j个单词的一种词向量(虽然实际中不用)。
从前向后 根据上述公式计算出C个输出向量之后,在每个\(V\)维向量中选取概率最大的作为输出的单词,这样根据输出单词\(w_I\) 就得到了\(C\)个输出单词,也就达到了根据单词预测上下文的目的。
下面开始介绍SG的反向传播训练的过程,这个跟前面的有些许的不同, 首先是损失函数:
\[\begin{align*}E &= -\log P(w_{1},w_{2},...,w_{C}| w_I) \\ &= - \log \Pi_{c=1}^{C}P(w_c|w_i) \\ &=-\log \Pi_{c=1}^{C} \frac{\exp (u_{c,j})}{\sum_{k=1}^{V} \exp(u_{c,k})} \\ &= -\sum_{c=1}^{C}u_{j_c^{*}} + C \cdot \log \sum_{k=1}^{V} \exp(u_{k}) \end{align*}\]
前面说过输出的C个词是相互独立,因此\(P(w_1,w_2,...,w_C|W_I) = \Pi P(w_c|w_I)\), 此外\(j_c^{*}\)的含义同One-Word Model 中的\(u_{j^{*}}\) 一样,都代表训练的真实的输出单词在词汇表的下标。下面开始从后向前求梯度,对第c个词对应的多项分布的第j项的梯度:
\[\frac{\partial E}{\partial u_{c,j}} = y_{c,j} - t_{c,j}\]
然后考虑\(W^{'}\)的梯度,考虑到C个多项分布产生影响,因此需要求和:
\[\frac{\partial E}{\partial w^{'}_{ij}}= \sum_{c=1}^{C}\frac{\partial E}{\partial u_{c,j}} \frac{\partial u_{c,j}}{\partial w_{ij}^{'}} =\sum_{c=1}^{C}(y_{c,j}-t_{c,j})\mathbf{h_{i}} = Q_j \mathbf{h_i}\]
跟CBOW一样,为了方便书写定义\(Q_j = \sum_{c=1}^{C}(y_{c,j} - t_{c,j}), \ j = 1,2,3,...,V\),矩阵Q的维度是$V1 $
有了梯度,就可以利用梯度下降 更新\(w_{ij}^{'}\):
\[w_{i,j}^{'}={w_{ij}^{'}}^{(old)} - \eta Q_j\mathbf{h}_i\]
或者写成词向量的形式,其实就是\(W^{'}\)的一列:
\[v_{w_j}^{'} = {v_{w_j}^{'}}^{(old)} - \eta Q_j \mathbf{h}, \ j = 1,2,3,...,V\]
接着考虑对隐层神经元的梯度:
\[\begin{align*}\frac{\partial E}{\partial \mathbf{h}_i} &=\sum_{c=1}^{C}\sum_{j=1}^{V} \frac{\partial E}{\partial u_{c,j}} \frac{\partial u_{c,j}}{\partial \mathbf{h}_i} \\&=\sum_{c=1}^{C}\sum_{j=1}^{V}(y_{c,j}-t_{c,j}) w^{'}_{ij} \\ &= \sum_{j=1}^{V}Q_jw^{'}_{i,j}=W^{'}_{i} \cdot Q \end{align*}\]
因此跟One-Word Model一样整合成向量的形式:
\[\frac{\partial E}{\partial \mathbf{h}} = W^{'} \cdot Q\]
考虑到输入只有一个词,因此跟One-Word Model 一样: \(\mathbf{h} = {v_{w_I}}^T\), 因此每次训练更新词向量矩阵\(W\)的一行:
\[v_{w_I}^T = v_{w_I}^T - \eta W^{'} \cdot Q\]
到此SkipGram模型的前向推理与后向参数的训练也介绍完毕了。
优化
复杂度
前面的CBOW与SG模型是标准的word2vec模型,或者说是神经语言模型的简化版,去掉了隐层的激活函数,其余的变化不大,因此训练效率还是很低的。我们分析下训练的复杂度。首先明确需要学习的两个词向量矩阵\(W, W^{'}\),从前面的推导中知道对于每一个训练样本,CBOW更新\(W\)的\(C\)行,SG更新\(W\)其中一行,也就是每次更新有限个词的词向量。但是对于\(W^{'}\)则不同了,正如前面一直提到的,无论是CBOW还是SG,对每个训练样本(或者Mini Batch)从梯度更新中需要对\(W^{'}\)的所有\(V \times N\)个元素,也就是词汇表中所有\(V\)个单词都需要更新词向量,考虑现实任务词汇表一般是几十万,上百万千万级别的, 这个计算成本是巨大的。
关于计算成本大的原因,除了上面提到的训练部分,还有就是在每次前向计算的时候,隐层到输出层的softmax函数计算输出层\(V\)个元素,计算量也是很大,这样整个模型现实意义不大。
考虑到计算量大的部分都是在隐层到输出层上,尤其是\(W^{'}\)的更新。因此word2vec使用了两种优化策略: Hierarchical Softmax 和 Negative Sampling。二者的出发点一致,就是在每个训练样本中,不再完全计算或者更新\(W^{'}\)这个矩阵。二者都不再显示使用\(W^{'}\)这个矩阵。因此这也就解释了前面说的为什么不用\(W^{'}\)作为最终词向量。
在多一句,其实上述训练和推理的复杂度很大的根本原因是softmax的分母上的\(\sum\),因此在求梯度的时候,就会有\(V\)次的计算。因此下面的两种方法其实是对softmax的优化,不仅仅限制在word2vec.
两种优化方式使得word2vec的训练速度大大提升,并且词向量的质量几乎没有下降,这也是word2vec在NLP领域如此流行的原因。 下面依次介绍这两种优化算法。
Hierarchical SoftMax
首先Hierarchical SoftMax(HS)并不是word2vec提出来的, 而是之前Bengio在2005年最早提出来专门为了加速计算神经语言模型中的softmax的一种方式, 这里介绍如何在word2vec中使用. HS主要基于哈夫曼树(一种二叉数)将计算量大的部分变为了一种二分类的问题. 先看下面的图, 原来的模型在隐层之后通过\(W^{'}\)连接输出层, 现在HS则去掉了\(W^{'}\), 隐层\(\mathbf{h}\)直接与下面的二叉树的root节点相连:
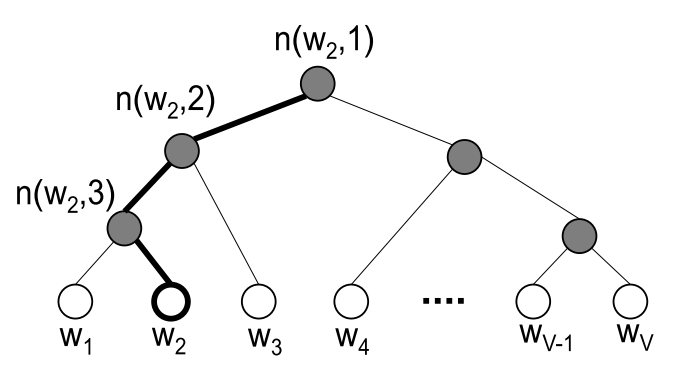
其中图中白色的叶子节点表示词汇表中所有的\(|V|\)个词, 黑色节点表示非叶子节点, 每一个叶子节点也就是每一个单词, 都对应唯一的一条从root节点出发的路径. 而我们的目的是使的\(w=w_O\)这条路径的概率最大,即: \(P(w=w_O | w_I)\) 最大, 此时每一个分支都代表一个选择, 向左转还是向右转. 所以如何判断向左还是向右呢? 我们用\(n(w,j)\)表示从root到叶子节点\(w\)的路径上的第\(j\)个非叶子节点, 并且每个非叶子节点都对应一个向量\(v^{'}_{n(w, j)}\), 维度与\(\mathbf{h}\)相同, 然后使用一个sigmod函数: \(\sigma(x)= \frac{1}{1+\exp(-x)} \in [0, 1]\), 结合向量的内积, 来判断该向左还是向右, 如下, 第n个节点向左 以及向右的概率定义:
\[\begin{align*}P(n, left ) &= \sigma({v^{'}_{w}} \cdot \mathbf{h}) \\ p(n, right) &=1-\sigma(v^{'}_w \cdot \mathbf{h}) = \sigma(-v_{w}^{'} \cdot h) \end{align*}\]
有了上述的概率, 我们可以重新定义\(P(w_O|w_i)\)了:
\[P(w=w_O|w_I)= \Pi_{j=1}^{L(w)-1}P(\sigma(I(n(w,j+1==left) v^{'}_{w} \cdot \mathbf{h} ))\]
其中\(I()\)是指示函数, 条件成立值为1, 反之为-1. 而\(L(w)\)表示整条路径的长度, 这样整个概率就是从root节点到叶子节点这条路径的概率, 这样我们在训练的时候, 通过训练样本来更新非叶子节点的参数\(v{'}_{w}\).
举个例子, 比如上图中的加粗的黑色路径: \((n(w_2,1), n(w_2, 2), n(w_2, 3), w_2\) , 就是说假设有一个训练样本是\((w_I, w_2)\), 我们需要使得\(P(w_O=w_2|w_I)\)概率最大:
\[\begin{align*}P(w_2=w_O) &= P(n(w_2,1), left) \cdot P(n(w_2,2), left) \cdot P(n(w_2, 3), right) \\ &= \sigma({v^{'}_{n(w_2,1)}}^T \mathbf{h}) \cdot \sigma({v^{'}_{n(w_2,2)}}^T \mathbf{h}) \cdot \sigma(-{v^{'}_{n(w_2,3)}}^T \mathbf{h}) \end{align*}\]
并且在一个非叶子节点处, 向左向右的概率和为1, 因此一直分裂下去,最后的和肯定还是1. 因此可以很容易得到:
\[\sum\limits_{j=1}^{V}P(w_j=w_O) =1 \]
这一点的证明是有必要的, 因为在原始的softmax本身保证了所有单词的概率和是1, 而通过上式也知道了通过HS得到的输出层仍然是一个概率多项分布, 输出所有的单词概率和为1.
讲完了从前向后的如何得到输出单词的概率的过程, 下面开始后向传播的训练过程. 首先需要明确的是训练的参数: 输入层与隐层的词向量矩阵\(W\), 以及二叉树的非叶子节点对应的向量\(\{v{'}_{n(w,j)}, j =1,2,3,..,L(w)-1\}\).
为了书写方便,下面简化一部分的符号: 用\([I]\)表示前面的指示函数\(I(n(w,j+1)==left)\), 使用\(v^{'}_{j}\)表示\(v^{'}_{n(w,j)}\)
对于一组训练数据, 损失函数的定义与前面相同, 最大似然(注意这里以One-Word Model为例,CBOW与Skip-Gram按照上述的思路完全一样):
\[E = -\log P(w=w_O|w_I) = - \sum\limits_{j=1}^{L(w)-1}\log \sigma([I] {v^{'}_{j}}^{T} \mathbf{h})\]
之后便可以逐项求梯度了, 先考虑\(v^T \mathbf{h}\), 注意\(\frac{\partial \sigma(x)}{x} = \sigma(1-\sigma)\): \[\begin{align*} \frac{\partial E}{\partial v^{'}_j \mathbf{h}} &= (\sigma([I] {v_{j}^{'}}^T \mathbf{h}))[I] \end{align*}\]
之后对\([I]\) 分情况讨论, 可得: \(\frac{\partial E}{\partial {v^{'}_{j}}^T \mathbf{h}} = \sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j\) 这里如果[I]=1, 那么$t_j =1 $, 否则 \(t_j=0\) , 这个公式与前面的\(y_j-t_j\)很类似, 可以理解为预测值与实际值的差别。
有了上述的梯度,就可以很简单的求出\(v^{'}\)的梯度了:
\[\frac{\partial E}{\partial v^{'}_j} = \frac{\partial E}{\partial {v^{'}_{j}}^T \mathbf{h}} \frac{\partial {v^{'}_{j}}^T \mathbf{h}}{\partial {v^{'}_{j}}^T} = (\sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j) \mathbf{h}\]
有了梯度,便可以更新了, 具体公式还是梯度下降:
\[{v^{'}_{j}}^{(new)} = {v^{'}_{j}}^{(old)} - \eta (\sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j) \mathbf{h},\ j=1,2,3,...,L(w)-1\]
也就是说对于一个训练样本, 我们只需要更新\(L(w)-1\)个向量就好了, 而未优化的版本需要更新\(V\)个, 相当于时间复杂度从\(O(V)\)降到了\(O(\log V)\) , 这个提升还是非常大的, 同时在考察空间复杂度,HS的二叉树的非叶子节点有\(V-1\)个,也就是我们需要\(V-1\)存储\(v^{'}_{j},\ \ j=1,2,3..V-1\) ,优化之前则是\(V\)个, 空间复杂度相同, 但是时间复杂度却大大降低。
然后考虑隐层\(\mathbf{h}\)的梯度,因为我们的优化目标都是在隐层到输出层,因此前面的几乎不变, 跟One-Word Model 一样,路径上的非叶子节点的表达式都含有\(\mathbf{h}\),因此需要对梯度求和:
\[\begin{align*} \frac{\partial E}{\partial \mathbf{h}} &= \sum\limits_{j=1}^{L(w)-1} \frac{\partial E}{\partial {v^{'}_{j}}^T \mathbf{h}} \frac{\partial {v^{'}_{j}}^T \mathbf{h}}{\partial \mathbf{h}} \\ &=\sum\limits_{j=1}^{L(w)-1}(\sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j)\cdot v^{'}_{j}\end{align*}\]
其实跟前面很一样了, 只需要替代下导数就好了, 后面就不再赘述了。
整个Hierarchical Softmax的优化算法介绍完了,隐层到输出层的计算量从\(O(V)\), 利用二叉树(更加具体来说是哈夫曼树)降为了\(O(\log V)\).
Negative Sampling
相比Hierarchical Softmax用复杂的树形结构来对softmax进行优化, 负采样(Negative Sampling)更加直接简单。因为softmax的存在,在使用梯度下降的时候,每个训练样本需要更新\(V\)个向量,这是根本问题。因此负采样NS仅仅更新一小部分向量,一般是5-20个,可以手工设定,而非全部\(V\)个(一般来说V都是几万到几百万的量级)。
再来考虑原始模型的训练过程,对于一个训练样本\((w_I, w_O)\), 我们要使得\(P(w=w_O|w_I)\)最大, 也就是说要使得输出层的其它单词的概率要比较小一些,基于这种思想, 我们将输出层的\(V\)个样本分为正例(Positive Sample)也就是\(w_O\)对应的项, 以及剩余\(V-1\)个负例(Negative Samples)。举个例子有个样本phone number,这样\(w_I=phone, w_O=number\), 正例就是number这个词, 负例就是不太可能与phone共同出现的词。
负采样的思想便是每次训练只随机取一小部分的负例使他们的概率最小,以及对应的正例概率最大。那么如何对负例进行抽样呢? 这里就需要定义一个noise distribution,有了分布\(P_n(w)\)就可以依据概率分布进行带权随机抽样了。 在word2vec中,作者直接使基于词的频次的词的权重分布:
\[weight(w) = \frac{coun(w)^{0.75}}{\sum _{u}count(w)^{0.75}}\]
相比于直接使用频次作为权重, 取0.75幂的好处可以减弱不同频次差异过大带来的影响,使得小频次的单词被采样的概率变大。
下面基于上面的思想,直接给出具体的损失函数:
\[E = -\log \sigma(v^{'}_{w_O}\mathbf{h}) - \sum\limits_{w_j \in \mathcal{W}_{neg}}\log \sigma(-v^{'}_{w_j}\mathbf{h})\]
\(\mathcal{W}_{neg}\)是负例单词集合。 上述公式跟原本的负采样的有些许差别,具体的推导细节可以参考这篇Goldberg, Y. and Levy, O. (2014). word2vec explained: deriving mikolov et al.’s negative- sampling word-embedding method. 这里不再赘述了。 只需要记住,NS也是对softmax函数做的优化,除了word2vec,在其他地方涉及到softmax的均可以采用类似的思想来重写目标函数。
有了损失函数,然后跟HS一样,用梯度下降的方法更新\(v^{'}\)即可,推导思路跟HS也是一样,分\(w_j\)是否等于\(w_O\)来讨论,最终得到的梯度公式与HS一模一样:
\[\frac{\partial E}{\partial {v^{'}_{j}}^T \mathbf{h}} = \sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j\]
这里的\(t_j\)含义跟前面提到的几次都相同。最后给出更新\(v^{'}\)的公式:
\[{v^{'}_{j}}^{(new)} = {v^{'}_{j}}^{(old)} - \eta (\sigma( {v^{'}_{j}}^T \mathbf{h}) - t_j) \mathbf{h},\ w_j \in \{w_O \} + \mathcal{W}_{neg}\]
从公式也可以看出,对于每个训练数据,每次只需要更新很少的几个向量,而非原始的\(V\)个,大大降低了训练复杂度。
跟HS相同,NS的优化也是对隐层到输出层的优化,因此前面输入层到隐层的梯度只需要做相应修改即可,没有影响,具体可以参考HS的公式,这里不再重复了。
到此为止,两种针对softmax的优化方式介绍完毕,简单对比一下两种方式:
- HS实现比较复杂, 需要借助哈夫曼树,而且HS是专门优化softmax的方法
- NS相对简单,仅仅是简单采样,NS则是一种概率采样的方法,属于NCE(Noise Contrastive Estimation)的一种简单形式,代码实现也很简单。 训练得到的词向量质量也很高,相对常用一些。
后话
这篇博客侧重word2vec的数学原理,主要是以神经网络的反向传播思路来解释训练过程,以及介绍了优化的原因和思路,基本上相当于一份对w2v相对全面解释的全家桶了,除了具体的代码实现细节,关于代码实现的话,以后看有没有时间整理吧。google官方的c实现的word2vec的代码还是非常非常值得一读的,只有600多行,里面用到了很多技巧,包括快速\(\sigma\)计算, 还有负采样的实现等等,使用异步梯度下降多线程训练(ASGD)等。
在4月份花了几天时间看完了google的两篇原始paper以及word2vec Parameter Learning Explained这篇以后,就想结合论文按照自己的理解整理一下, 不过当时仅仅列出了目录,写了个开头背景,之后因为课程,读NE的paper等各种事情,一直拖着到现在了。 这段时间趁出差期间反正没事,现在算是就把这个坑补上了。 有什么写的不严谨的地方,烦请指出。