继上一节的Aggregation和Bagging,这一节对那一堆的g函数的产生做更深的探究,对训练数据引入权重的机制(Weight-Based),加大错误数据的权重,缩小正确数据的权重,从而得到更加 Powerful的算法-AdaBoost
从Bagging引入权重
回想上节的Bagging,通过Bootstrap来生成多份的数据\(D_t\),这里面可能会有重复,例如:
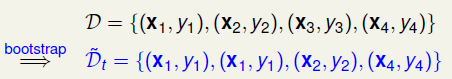
以分类为例,计算0/1误差: \(E_{in}={1\over4}\sum||y \neq h(x)||\)。现在引入新的变量: \(u_n\)表示\(\mathcal D\)中的第n个数据在采样得到的\(\tilde{\mathcal D_t}\)中的个数,对于上面的例子,则有:\(u_1=2, u_2=1, u_3=0,u_4=1\), 那么误差可以换一种方式写:\(E_{in}={1\over4}\sum u_n||y \neq h(x)||\)。这样就把\(u_n\)引入了错误函数中,可以表示某个数据的权重,这种思想在数据挖掘中很常见,在分类的时候,对于分错的数据,我们需要特别关注,因此把错误数据的重要性放大,或者说人为多复制几份错误数据放进去,这样再迭代的时候,错误数据就会变少了。
我们可以将权重引入一些之前的模型中,比如SVM:

未加权重之前,每个错误的惩罚系数为\(C\),现在加了权重可以理解为错误惩罚变为了\(Cu_n\), 同时也体现在\(\alpha_n\)的上限中。 在比如Logistic Regression中,同样可以引入权重:

这里可以理解为,在使用随机梯度下降优化的时候,同bagging,\(u_n\)代表取出的数据的份数。
更新权重
再次回到模型融合,在前一章的aggregation中,我们提到了如果\(g_1, g_2,...,g_T\)中效果差距越明显,那么通过融合可以取得更好的结果,现在考察怎么样才可以让\(g\)与\(g\)之间区分度更明显,考虑\(g_t\)与\(g_{t+1}\):
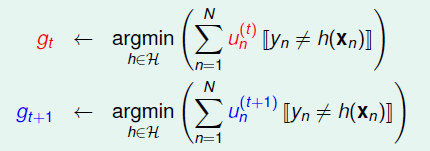
\(g_t\)的是通过权重系数为\(u^{(t)}\)中在假设空间中误差最下的h来得到的,\(g_{t+1}\)则是\(u^{(t+1)}\), 如果\(g_t\)在权重为\(u^{(t+1)}\)的条件下,表现不好的话,那么在\(t+1\)的时候,我们就不会选择出\(g_t\)或者与\(g_t\)很近似的h了,而是在\(u^{(t+1)}\)的条件下误差最小的\(g_{t+1}\),这样就会使得\(g_t\)与\(g_{t+1}\)更加diverse。 那么如何来衡量表现不好呢? 很简单的思路,在二分类问题中,表现不好那就是跟随机瞎猜一样,正确率50%,写成表达式便是:
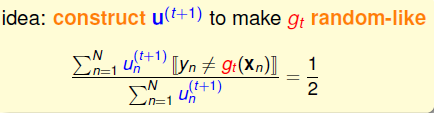
再剖析这个式子,因为可以将\(u_n\)理解为数据有多少份。在\(g_t\)中,即分子就是分类错误的数据个数,分母就是所有数据的个数了。因此我们需要的是,在\(u^{(t+1)}\)的条件下,正确的份数==错误的份数,那\(u^{(t+1)}\)应该与\(u^{(t)}\)有什么关系呢? 举个例子,假设在\(u^{(t)}\)下, 分类错误1126份,正确6211份,那么在\(u^{(t+1)}\)下,二者应该相等,那应该怎么办呢?看下面的几步:
\[\begin{align} & A = \sum u_n^{(t)}||y_n\neq g_t(x_n|| = 1126, \quad B= \sum u_n^{(t)}||y_n ==\ g_t(x_n)|| = 6211 \\ \Rightarrow &A*6211 = B*1126 \\ \Rightarrow &\left(\sum (6211*u_n^{(t)} \neq)\right) \mathbf = \left( \sum 1126 * u_n^{(t)} == \right) \end{align}\]
因此想要达到在\(u^{(t+1)}\)下,\(g_t\)正确率到50%,只需要做一个放缩即可:
- 错误的数据: \(u_n^{(t+1)} = 6211 * u_n^{(t)}\)
- 正确的数据: \(u_n^{(t+1)} = 1126 * u_n^{(t)}\)
一般来说,我们都是用比率来放缩,假设错误率是\(\epsilon_t\),那么根据上面的思路,就可以更新\(u_n^{(t+1)}\)如下:
- 错误数据: \(u_n^{(t+1)} = (1-\epsilon_t) * u_n^{(t)}\)
- 正确数据: \(u_n^{(t+1)} = \epsilon_t * u_n^{(t)}\)
\(g_t\)的效果是可以接受的,因此一般来说\(\epsilon_t < {1 \over 2}\),这样定性来说,其实就是在下一轮的g中,加强了上一轮分类错误数据的权重。
Adapive Boosting算法
除了上面使用\(\epsilon_t\)作为缩放系数之外,在实际中使用一种等价的方式,定义\(\blacklozenge_t = \sqrt{1-\epsilon_t \over \epsilon_t}\),之后采用下面的策略更新\(u^{(t+1)}\):
- 错误的数据: \(u_n^{(t+1)} = u_n^{(t)} \cdot \blacklozenge_t\)
- 正确的数据: \(u_n^{(t+1)} = u_n^{(t)} / \blacklozenge_t\)
意义也是一样的,因为\(\blacklozenge_t > 1\),因此每次对于错误数据加大权重,正确数据减少权重,从而得到一个同\(g_t\)不一样的\(g_{t+1}\)。
这样我们就可以得到了区分度较大的一堆\(g_1, g_2,....,g_T\),然后就可以用用线性后者非线性的融合方式进行融合。比较常用的是Linear Aggregation,即需要对\(g_t\)进行线性组合: \(G(\mathbf x ) =sign(\sum\limits_{t=1}^{T}\alpha_t g_t)\),下面开始考察如何确定\(\alpha_t\)。基本思路便是,效果好的\(g_t\)对应的权重\(\alpha_t\)应该大一点,反之应该小一点。 再回想\(\blacklozenge_t\)正好是正确率(\(1-\epsilon_t\))的单调增函数,因此在实际中,经常用: \(\alpha_t = \ln\blacklozenge_t\),这样的好处是在计算\(g_t\)的时候,就把其对应的权重\(\alpha_t\)得到了。比如两种极限情况:
- 如果随机乱分,\(\epsilon_t=0.5\),此时\(\blacklozenge_t=1\),那么\(\alpha_t=0\),也就是说坏的g分配0权重
- 如果\(\epsilon_t=0\),此时\(\blacklozenge_t=\infty\),那么\(\alpha_t=\infty\)也就是说好的g分配无穷大权重
最后一个问题,最初的\(u^{(1)}\)应该怎么确定? 因为是初始值,并不知道数据情况,因此一般情况直接将权重初始化为相同:
\[u^{(1)} = [ {1\over N}, {1 \over N},..., {1 \over N}]\]
这样AdaBoost算法就完整了,总结一下流程如下:

这个算法也叫Linear Aggregation On the Fly,当然也是属于Adaptive Boosting,叫boosting的原因是因为我们只需要开始有一个很弱的演算法\(\mathcal A\),然后通过一点点增加错误数据的权重,降低正确数据的权重,最后得到一个效果很好的分类器,因此一般也用三个臭皮匠赛过诸葛亮来形容Adaboosting。
VC 维保证
这里简单介绍AdaBoost算法的理论保证。有数学证明可以得到Adaboost的VC Bound:
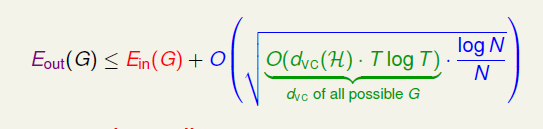
因为算法一共需要T个g,因此在第二项模型复杂度中多了\(TlogT\)这一项,其余不变。有实验证明如果每次的\(\epsilon_t < 0.5\)的话,也就是说不是乱猜的话, 只需要经过\(T= O(logN)\)次迭代就可以收敛到\(E_{in} = 0\)。
总结
为什么这个算法叫做Adaptive Boost(自适应提升)呢? 是因为我们一开始只需要一个很简单的弱分类算法,只要比随机分类好就行,也就是\(\epsilon_t <0.5\),然后通过每次加大错误数据的权重,着重训练错误数据,一点点可以提高正确率,直到收敛。这种算法最开始用在人脸检测上,并且取得了当时最好的效果。