前面的课程着重介绍某单一模型,比如逻辑回归,SVM等,从这一节开始以及接下来的3,4节的课程都是在介绍多个模型之间的融合得到一个新的模型的问题。
为什么要进行模型融合
我们针对某个问题,使用不同的演算法得到了很多模型g,个模型都会有自己擅长的部分,也有不擅长的部分,如果能够可以把它们混合起来,那新模型的效果就可能很好。假设我们已经得到了\(g_1,g_2,...,g_T\)等T个model,那我们怎么把它们混合为一个新的模型呢\(G(x)\)?方法很多,例如:
- 最简单的,直接在所有的模型里面,选择验证误差最小的作为最后的模型: \(G(\mathbf x)=\arg\min\limits_{t \in {1,2,..T}} E_{val}(g_t^{-})\)
- 直接采取所有\(g_t\)的意见,对它们同等信任,比如分类问题: \(G(\mathbf x) = sign(\sum\limits_{t=1}^{T}1 \cdot g_t(\mathbf x))\)
- 比上一种情况,再更近一层,给每个\(g\)不同的投票数目,也就是说它们权重不再相同\(G(\mathbf x)=sign(\sum\limits_{t=1}^T\alpha_t \cdot g_t(\mathbf x))\),这个权重\(\alpha_t \geq 0\)可以通过训练得到。
- 再特殊一点,根据不同的数据的特点,来赋予不同的权重: \(G(\mathbf x)=sign(\sum\limits_{t=1}^Tq_t(\mathbf x) \cdot g_t(\mathbf x))\), 其中\(q_t \geq 0\)。
除了上面的四种融合之外,还有很多其它的没有列举出来。其中第一种就是前面基石课程中的模型选择的做法,此外这里的\(g_{t}^{-}(\mathbf x)\)是指在减去了验证数据集之后的数据作为训练数据得到的模型。
换句话说,有几个很weak的假设空间,通过融合等手段,得到一个更加powerful的假设空间,从而得到效果更好的模型,如下:
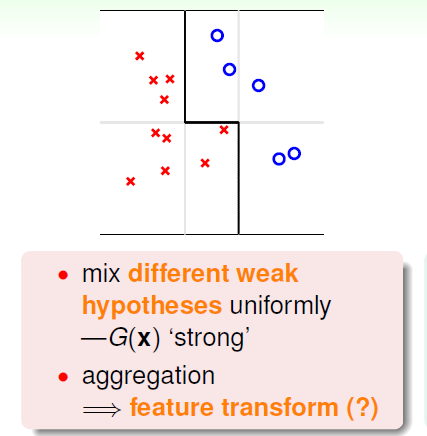
比如我们有一些只能划分水平与竖直方向的分界线的假设空间,如上图中的灰色的线,分类效果肯定很差,但是如果将这些弱的分类器组合起来,就可以得到一个不错的边界,如上图的黑色的线。因此看起来如果对多个模型进行一个合适的融合(aggregaton),或许就可以得到效果更好的模型。
Uniform Blending(均匀融合)
这一部分从误差的角度介绍最基本的Uniform Blending(均匀融合)的一些理论依据,Uniform Blending的分类的模型如下,实际上就是少数服从多数的原则:
\[G(\mathbf x)=sign \left( \sum\limits_{t=1}^{T}1 \cdot g_t(\mathbf x)\right)\]
回归模型如下,直接求T个模型g的结果的平均值:
\[G(\mathbf x)= {1\over T}\sum\limits_{t=1}^{T}1 \cdot g_t(\mathbf x)\]
下面以回归问题分析误差。
预期\(g_1,g_2,\cdots,g_T\)的效果应该参差不齐,比如一些\(g(\mathbf x)<f(\mathbf x)\),还有一些\(g(\mathbf x) > f(\mathbf x)\),这里的\(f(\mathbf x)\)是理想的未知的函数,这样通过融合平均下来得到的结果会更加准确。反过来,如果每个\(g\)的结果都差不多,那就没有必要做融合了。下面来分析融合前后的误差比较。
比较\(g_t\)与\(f\)的均方误差与融合之后的\(G\)与\(f\)的均方误差:

关于上述式子的展开有几个细节需要注意:
- \(avg(g_t) = {1\over T}\sum g_t = G\)
- f与avg无关
这样我们就可以得到下面的结论,(如果没有看过基石课程的话,这里的\(E_{out}\)可以理解为g与f的差距平方):
\[avg(E_{out}(g_t)) \geq E_{out}(G)\]
可以看出\(g_t\)的平均误差比融合之后的\(G\)要大,也就是说融合模型效果应该会更好。
基于上述的证明,现在考虑一个假想的极限情况,假设我们每次从数据分布中拿出N个数据\(\mathcal{D}_t\),然后通过演算法\(\mathcal {A(D_t)}\)得到\(g_t\),(因为每次的数据\(D_t\)都不一样,因此每个\(g\)的差别也就会变大,这也正是我们所期望的,得到不同给的模型)。如果数量T趋向于无穷大,我们就可以得到一个理想的\(\overline{g}\),它可以被认为在所有的数据得到的模型,可以体现出演算法\(\mathcal A\)的在所有的\(\mathcal D\)中的表现了
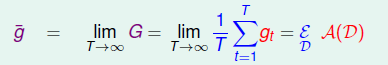
应用上面的结论,有:
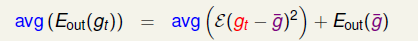
其中\(\overline{g}\)可以代表一堆\(g_t\)的达成的共识(consensus)。式子的第一部分称为我们的演算法\(\mathcal A\)的在不同的数据集上\(D_1,...D_T\)的平均表现,右边式子\(E_{out}(\overline g)\)的第二部分就是共识的误差,一般称为 bias,描述的是共识与理想函数f的差距;第一部分\(avg\)则描述的是一种方差,\(g_t\)与\(\overline g\)的平均差别,一般叫做variance, 因此衡量一个演算法的表现,就是bias+varience。 那么我们的Uniform Blending其实就是减少varience的过程。
关于这部分\(\mathcal {A,D},g\)等概念,请见机器学习基石笔记
Linear Blending(线性融合)
上面的均匀融合每个g的作用相同,最后的模型可能会变得中庸一些,稍加改变,如果每个g都一个不同的投票权重,效果应该就会更好,这就是线性融合(Linear Blending):
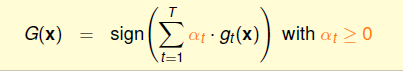
假设我们已经得到了T个\(g_t\),那么应该如何确定\(\alpha_t\)呢,思路就是\(\min E_{in}\),这个式子之前其实遇到过,回想在Linear Regression+Transformation的情况,使用均方误差:
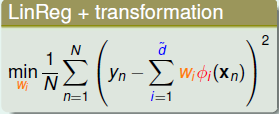
再看看Linear Blending的做回归时候的目标函数:

二者其实是很类似的,我们也可以将\(g_t(\mathbf x)\)作为一种feature transform,这样我们将原始数据转换为: \((\mathbf z_n, y_n), \mathbf z_n=(g_1(\mathbf x_n),...,\mathbf g_T(\mathbf x_n))\),从这个角度来看与Linear Regression就完全一样了,这时候就可以直接用线性回归的方式来求解\(\alpha\)
然而有一点需要注意的是,Linear Blending有一个约束\(\alpha_t \geq 0\),因为每个模型的投票数不能为负数,而Linear Regression则没有这个约束。其实可以从这角度考虑,来去掉这个限制。对于那些\(\alpha_t < 0\),我们可以认为是\(\alpha_t g_t = |\alpha_t|(-g_t)\),这样就没有问题了,在物理意义上也可以解释,比如在一个分类问题中,对于那些效果很差的g,我们取其相反数,那么就可以得到一个好的g。到此,Linear Blending 与 Linear Regression + Feature Transform 等价了。
求出了\(\alpha\),我们还需要注意下如何选择一堆的\(g_t\):
\[g_1 \in \mathcal H_1, g_2 \in \mathcal H_2...g_T \in \mathcal{H}_T\]
一种思路是求出每个\(\mathcal H_t\)中\(E_{in}\)最小的\(g\),第二种则是\(E_{val}\)最小的\(g^{-}\),显然为了防止过拟合,应该使用\(g^{-}\)。
注: \(g^{}-\)就是使用总数据的N-K个数据做训练,然后用K个数据做验证,选择验证中err最小的g,而非训练误差最小的g。
简单总结下Linear Blending的流程:
- 通过\(\min E_{val}\)的方式训练得到T个\(g^{-}\)
- "特征转化": \(\mathbf z_n = \phi^{-}(\mathbf x_n) = (g_1^{-}(\mathbf x_n), g_2^{-}(\mathbf x_n)...g_{T}^{-}(\mathbf x_n))\),数据变为\((z_n, y_n)\)
- Blengding: 计算\(\alpha\), 现在是一个很简单的线性问题了,通过之前的线性回归,逻辑回归等方法得到投票权重
- 最终的模型: \(G(\mathbf x)=LinearModel(\sum\limits_{n=1}^{N}\alpha^T \phi(\mathbf x))\)
注: 最后的\(\phi=(g_1,g_2....)\)而非\(g^{-}\),因为通常,使用N-K个数据训练得到\(\min E_{val}\)得到最好的\(g^{-}\),之后,一般再用全部的N个数据重新训练一遍,得到\(g\),因为一般数据量越大,模型泛化性能就好.
其实除了Linear Blending之外,在得到\((z_n, y_n)\)之后,完全可以用一些其它的非线性的模型去解决这个分类或者回归问题,这样可能更加Powerful,但是也就更容易过拟合,因此还是那句话: Linear First。
模型融合在实际数据挖掘中,还是很常用的。在2011的KDDCup上,林老师的台大队伍最后加了使用测试数据的linear blending在比赛封榜最后一个小时,成功逆袭,从第二成为第一,夺得冠军。
Bootstrap Aggregation(Bagging)
前面的一堆的\(g\)是通过很多份数据来得到的,但是如果我们只有一份数据呢,也就是只有N个样例,怎么来得到区分度更好的\(g\)呢,下面利用一种叫Bootstrap的采样方式来利用已有的数据来采样得到新的数据集。
Bootstrapping: 在已有的\(\mathcal D\)中每次有放回的取样,重复N次,得到一组数据\(D_t^{t}\), 包含N个样例,这个采样过程便叫做Bootstrap
上面的原理很简单,这样得到的每个\(D_t\)中有很大的可能出现重复数据,不过这个不影响,反正我们有很多的\(g\),之后再用上面的Blending的方式进行Aggregation,这种方式一般叫做 Bootstrap Aggregation,通常简称Bagging。 这种方式在实际中应用很多,尤其是数据不足的情况下。
附
这部分与机器学习基石课程中的一些基础的理论有很大的关系,包括算法,模型,假设空间, \(E_{in}, E_{out}\)等概念,还有validation的过程等。 可能是因为这部分还没有写代码实践,因此理解的可能还不到位,整理的有点乱,希望能看到这里的同学多指正。