2016.11.30更新: VC维
上一节,我们把 leaning问题归结到了我们提到需要证明dichotomies是多项式的,这样就可以保证在N比较大的时候,BAD DATA出现的概率是很小的,这样就说明我们的 learning学到了东西,可以用来预测。
下面求证\(m_{\mathcal{H}}\) 是多项式
最大的最大:B(N,K)
我们提到了 break point 是第一个满足: \(m_{\mathcal{H}}(N) < 2^N\) 的N,那我们可以得到什么信息呢? 假设 \(K=k\),首先K之前的均被\(\mathcal{H}\) shatter掉了, K及K之后的则没有,如下:
- \(N < K\): every $m_{}{N} = 2^N $
- \(N \geq K\): every \(m_{\mathcal{H}}(N) < 2^N\),对于 N > K的D, 显然\(m < 2^N\)
举一个简单的例子: 假设K=2, 求\(m_{\mathcal{H}}(N=3)\), 如下: 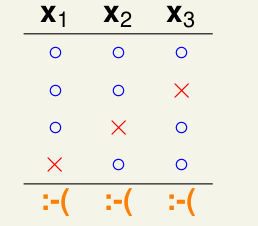
经过实验发现,其最大为4, 因为k=2,限制了\(x_1, x_2, x_3\)中任意两个点都不能被\(\mathcal{H}\)给shatter了,这里就会发现 break point的作用了, 限制\(m_{\mathcal{H}}\)的上界。下面定义Bounding Function:\[B(N,K) = max(m_{\mathcal{H}}(N)), s.t. break\ point = K \]
因为成长函数\(m_{\mathcal{H}}(N)\)就是\(\mathcal{H}\)对输入\(x_1...x_N\)可以产生的dichotomies的最大值, 所以B(N,K)就是最大值的最大。
如下,我们分情况讨论: \[ \begin{align} B(N, 1) &= 1 \\ B(N, k) &= 2^N,\ N < k\\ B(N, k) &= 2^N-1,\ N=k \\ B(N, k) &= ? \ N>K \end{align} \]
在课程中,老师举了一个求B(4,3)=11的例子: 通过归纳法的思想,推导出N>K下,\(B(N,K)\)的递推公式:\[B(N,K) \leq B(N-1,K) + B(N-1, K-1)\] 正如下面的图所描述的: 
下面我们根据递推式,通过数学归纳法来证明:\(B(N,K) \leq \sum\limits_{i=0}^{K-1} \left( \begin{array}{c}N \\ i \end{array}\right)\).
当N=1或者K=1时,显然成立。假设当\(N=N_0\)时, \(B(N_0,K) \leq \sum\limits_{i=0}^{K-1} \left( \begin{array}{c}N_0 \\ i \end{array}\right)\),则当\(N=N_0 + 1\)时: \[ \begin{align} B(N_0 +1, K) & \leq B(N_0, K) + B(N_0, K-1) \\ & \leq \sum\limits_{i=0}^{K-1} \left( \begin{array}{c}N_0 \\ i \end{array}\right) + \sum\limits_{i=0}^{K-2} \left( \begin{array}{c}N_0 \\ i \end{array}\right) \\ & \leq 1 + \sum\limits_{i=1}^{K-1} \left( \left( \begin{array}{c}N_0\ i \end{array} \right) + \left(\begin{array}{c}N_0\\i-1 \end{array}\right) \right) \\ & \leq 1 + \sum\limits_{i=1}^{K-1} \left( \begin{array}{c}N_0+1 \\ i \end{array} \right) \\ & \leq \sum\limits_{i=0}^{K-1}\left( \begin{array}{c}N_0+1 \\ i \end{array} \right) \end{align} \] 得证: \(B(N_0,K) \leq \sum\limits_{i=0}^{K-1} \left( \begin{array}{c}N_0 \\ i \end{array}\right)\) 很明显,\(B(N_0,K) \leq \sum\limits_{i=0}^{K-1} \left( \begin{array}{c}N_0 \\ i \end{array}\right) = O(N^{K-1})\), 多项式复杂度,曙光出现。到这里,我们需要需要理一下思路了。 \[P\left[ | E_{in}(h) - E_{out}(h)| > \epsilon \right] \leq 2 m_{\mathcal{H}}(N) exp(-2\epsilon^2N)\] 我们知道当出现BAD DATA时候, 会导致\(E_{in}\)与\(E_{out}\)变大,此时learning并不可行,因此我们开始计算BAD DATA出现的概率,它与\(\mathcal{H}\)的数目有关系,而很多情况,h都是无限的,于是我们转为求h中的类别数目,我们定义了\(dichotomies\) 以及\(m_{\mathcal{H}}(N)\), 也就是上述的不等式,在一些简单的情况下,\(m_{\mathcal{H}}(N)\)是很容易求的,比如postive rays里面, \(m_{\mathcal{H}} = N+1\) 等,但是很多我们并不能求出来,比如2D percertron,(PLA), 这个时候,我们定义break point 转而去求\(m_{\mathcal{H}}\)的上界\(B(N,K)\),最终我们证明了\(B(N,K) = O(N^{K-1})\)。到这里我们基本证明以Perceptrons为例,说明了为什么机器可以学习,为什么训练数据集越大,测试效果越好。 不过还有点小问题,在下面说明。
VC Bound
我们前面基本都在围绕这训练数据也就是\(\mathcal{D}\)或者\(E_{in}\)讨论,把\(\mathcal{H}\)根据在\(\mathcal{D}\)上的表现分门别类,这样\(E_{in}\)就会是有限个,但是却忽略了每一个\(h\)的\(E_{out}\) 是不一样的,也就是说\(E_{out}(h)\)是无穷多个的,所以说上述的不等式是不太严谨的,实际上的不等式是下面的: \[ \begin{align} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \end{align} \] 证明的主要原则是,如果某个\(E_{in}\)与\(E_{out}\)的差别很大时,那么我们重新找一份数据集\(D^{'}\), 那么\(E_{in}^{'}\)也会有很大的几率与\(E_{in}\)差别很大。 具体证明还没搞太明白,先记下了。另外,上面的不等式就是VC-bound.
VC Dimension
下面我们基于break point 给出 VC Dimension(VC 维)的定义:\[d_{VC}(\mathcal{H})= \max\limits_{N} m_{\mathcal{H}} = 2^N\]也就是break point K的前一个: \(d_{VC} = K - 1\)(break point存在的前提下)。我们可以看看上述的4种\(\mathcal{H}\)的VC Dimension 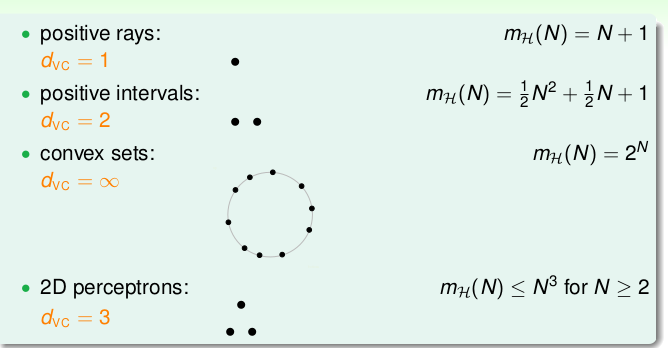
下面我们看看VC维可以给我们带来什么信息。已知成长函数\(m_{\mathcal{H}} \leq N^{k-1}=N^{d_{vc}}\),然后代入上述的VC Bound:
\[\begin{align*} \mathbb{P}[BAD] &= \mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] \\ &\leq 4m_{\mathcal{H}}(2N)exp(-\frac{1}{8}\epsilon^2N) \\ &= 4(2N)^{d_{vc}} exp(-\frac{1}{8}\epsilon^2N)\end{align*}\] 那么怎么样才可以说明机器学到了东西呢?有以下三点:
- 存在break point即 \(d_{vc}(\mathcal{H})\)是有限的,这样的\(\mathcal{H}\)才是good的
- 训练数据足够多: N 够大,这样vc bound 可以约束\(E_{in} = E_{out}\)
- 算法\(\mathcal{}A\) 可以找到一个\(E_{in}\)最小的h
这样我们就可以说 learned something。以2D Perceptron 为例如下:

当然实际中,\(E_{in}\)很难为0。那我们可以怎么去理解这个VC 维度呢? 由定义可以知道,VC 维与学习算法\(\mathcal{H}\),输入数据\(\mathcal{D}\),以及目标的理想函数\(f\)都是无关的, 它是假设空间\(\mathcal{H}\)的一个描述,刻画出了\(\mathcal{H}\)的powerfulness,因为\(d_{vc}\)越大,可以shatter的点就越多,能力就越强,也就是说我们的\(d_{vc}(\mathcal{H})\)越大,那么就越可以保证存在一个 h,使得\(E_{in}(h)\)越小。
那我们应该如何去求解VC 维呢? 总不能一个一个试,看看能不能被shatter掉。这时候就引入了模型自由度的概念。我们定义模型当中可以自由变动的参数的个数,也就是需要求的参数的个数作为模型自由度,比如在 PLA中,参数为\(w_0,w_1...w_d\) 一共有\(d+1\)个,那么模型的自由度就是\(d+1\),同时我们也知道假设空间\(\mathcal{H}\)的VC 维是 \(d+1\)。这不是巧合,有个经验规律:VC维 约等于 模型的自由度,即参数的个数。以后我们就可以用模型自由度近似代替\(d_{vc}\)的数值了。
再次回到VC Bound:\[\mathbb{P}[\exists h \in \mathcal{H}\text{ s.t. } |E_{in}(h)-E_{out}(h)|\gt \epsilon] = 4(2N)^{d_{vc}} exp(-\frac{1}{8}\epsilon^2N)\]其中等式右边为坏数据发生的概率,我们设为\(\delta\),那么好数据的概率就是\(1-\delta\),在统计学中,这个\(1-\delta\)又叫做置信度。有了\(\delta\),我们可以反解出误差率(也叫泛化误差)\(\epsilon\):
\[ \epsilon= \sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \]它就是\(E_{in}\)和\(E_{out}\)的差距,对于好数据来说,有很大的几率:\(\| E_{in} - E_{out} \| < \epsilon\),代入 \(\epsilon\)即:
\[E_{in}(g)-\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \leq E_{out}(g) \leq E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta})} \]其中根号里面的式子\(\Omega (N,\mathcal{H},\delta)=\sqrt{...}\) 称为model complexity(模型复杂度)。自始至终我们最关心的肯定是\(E_{out}\),我们的目标就是让它越小越好,这样才可以在未知数据中表现的好,从不等式中,我们可以看出\(E_{out}\)的上限会被模型复杂度影响。根据上述的不等式,有了下述的一个关系图:

这个图很重要,也很常用,随着\(d_{vc}\)的上升,\(E_{in}\)越来越低,但是 model complexity 会一直变大,这样就会导致\(E_{out}\)也会慢慢变大!这并不是我们想要的结果。也就是说并不是你的\(\mathcal{H}\)越强大越好其实这个就对应后面讲的过拟合的问题,因此我们需要的是图中的\(d_{vc}^{*}\)的位置的模型,一个折中的选择,这个也可以对应奥卡姆剃刀理论,简单至上。
最后再说明下样本复杂度的影响,以一个例子做说明,如下:

就是对于2D percetron,给定了误差率\(\epsilon\),置信度\(1-\delta=0.9\)。让求需要多少数据量才可以满足条件。很简单直接代入公式就好了,我们可以看出,大概需要3w左右也就是10000倍的\(d_{vc}\)的训练数据量才可以达到90%的置信度,这可能有点难以接受。幸亏这只是上界,在实际经验中,仅仅需要10倍的\(d_{vc}\)就可以达到要求。我们发现,VC Bound 的 losseness是十分松弛的,这正是因为我们一直都是再取上界的上界,都是在进行放缩操作,比如\(m_{\mathcal{H}}(N) \leq N^(k-1)\)。再加上VC Bound的通用性,与数据的分布什么的都没关系。
总结一下的话, 其实就是介绍了VC维的定义,以及我们可以用模型自由度来近似代替VC维的大小,最后介绍了VC维以及VCbound 带给我们什么信息,它与训练误差,测试误差之间的联系等。VC 维是个很重要的概念,是机器学习可以学习的理论基础,我们有了合适的\(d_{vc}\),有足够的训练数据量,有一个好的算法可以找到一个\(E_{in}\)最小的h,就说明我们的机器学到东西了。总算总结完了,VC-Dimension 这个坑到今天总算填上了。