learning的两个问题
从上一讲我们知道，我们知道learning可以分为两个问题: 如下 其实，training过程就是解决第二个问题的过程。 testing的过程则是解决第一个问题的过程。
- 能否保证\(E_{in} \thickapprox E_{out}\)
- 能否保证\(E_{in} \thickapprox 0\)
首先把Learning的框架摆上来: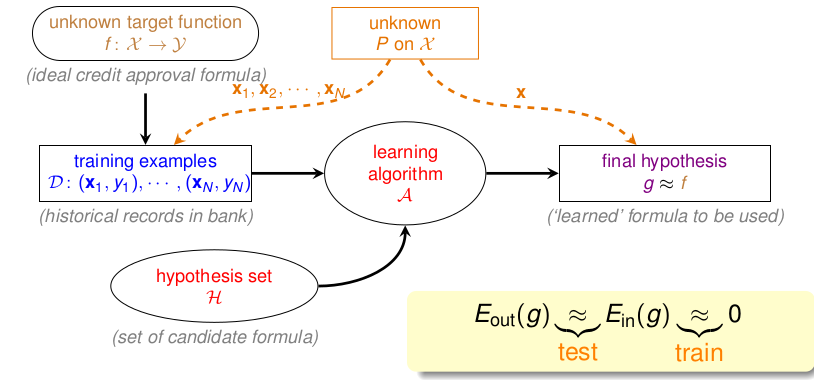 
在上一节，我们把问题归结到了 BAD DATA的概率问题上，如果我们可以知道坏数据出现的概率很小的话，那我们就可以保证第一个问题，那么再次选择最小的\(E_{in}\)这样我们就完成了Learning的目标了。
M的实际有效值
PAL感知机
\[ P[ | E_{in} - E_{out} | > \epsilon ] \leq 2 \cdot M \cdot exp \lgroup -2 \epsilon^2N\rgroup \] 从式子中，可以看出当M比较小的时候，即假设空间\(\mathcal{H}\)中可以选择的函数比较少，这样就很容易保证坏数据出现的概率很小，但是因为选择性太少了，我们无法保证\(E_{in}\)尽可能小。但是M比较大的时候，选择多了， 但是却让坏数据概率大了。 现在，我们考虑一下， BAD DATA的推导公式: \[ P[ BAD | \mathcal{H}] \leq_{union bound} P(BAD | h_1) + P(BAD | h_2) + ... + P(BAD | h_M) \] 这里面有个问题，在计算右边时，直接对每一个\(h\)求和，这个是上界，也就是当每一项都独立时，该等号才成立，但是实际情况下，并非这样，比如\(h_1, h_2\)两个很相似的\(hypothsis\), 也就是说，满足如下两个要求: - \(E_{out}(h_1) \thickapprox E_{out}(h_2)\) - \(E_{in}(h_1) \thickapprox E_{in}(h_2)\)
也就是说，对于大部分的\(\mathcal{D}\)来说，\(h_1\)和\(h_2\)的输出是很类似的，或者说，可以把它们两个当作一类。也就是说， 当\(h_1\)遇到 BAD DATA时，\(h_2\)会遇到。这样\((BAD|h_1)\) 与\((BAD|h_2)\)并不是独立事件，而是很多\(\mathcal{D}\)造成重复。如下: 我们记 \(h_i\)遇到 BAD DATA为事件\(\mathcal{B}_i\), 这样实际情况就会如下: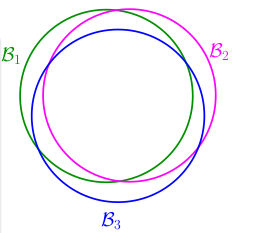 
也就是说我们上面的 \(unionbound\) 是 over-estimating的，过大估计了。这样好像就看到了曙光，即使\(M\)无穷大，但是实际上很多的重复部分，因此我们只需要知道类别的数目是不是就可以代替无穷大的\(M\)了，先看几个简单的例子.
在PAL中，\(\mathcal{H} = \{ all \ lines \ in \ \mathcal{R}^2 \}\), 首先有无穷多条直线，但是看看对不同的输入,看看有几类呢？
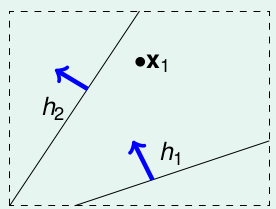
当输入只有一个点的时候，我们可以发现，只有两类点:
- \(h_1-like(x_1) = o\) 与 \(h_1\)类似，将\(x_1\)归为 o
- \(h_2-like(x_2) = x\) 与 \(h_1\)类似，将\(x_1\)归为 x
再看看输入有两个点的情况: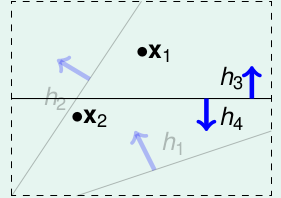 
我们发现有如下四类直线: 得到如下的结果:
输入有三个的时候，画画可以最多有8种:(当三个输入点在一条直线上，只有6种）
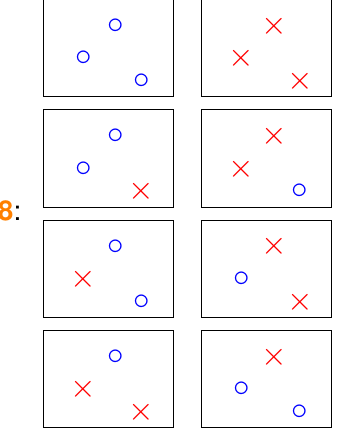
输入有4个点的时候，不一样了，不是\(2^4\)种了，而是只有14种,下面的两种无法用二维直线得到:
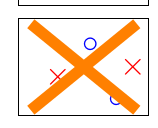
以及其对称图形 那么问题来了，对于N个输入的input,到底有多少类直线呢，首先肯定不会超过\(2^N\)，因为每个点要么被分到O，要么被分到X。综合上面说的，我们把M可以替换为实际有的类别数目，这样我们的之前的公式就可以改写为： \[ P[ | E_{in} - E_{out} | > \epsilon ] \leq 2 \cdot effective(N) \cdot exp \lgroup -2 \epsilon^2N\rgroup \]
下面就是如何求这个\(effective N\)了
Dichotomies:
我们想要的是\(\mathcal{H}\)里面的所有的\(h\)可以在\(\mathcal{D}\)上产生多少种结果，也就是上面的 \(effective N\)。每一种结果我们称为一个Dichotomies,比如上述\(\{ OOXX\}\) 就是一个dichotomies,很明显，对于输入\((x_1, x_2...x_N)\), 最多有\(2^N\)个dictomies。每一个dictomies都是一类\(h\)产生的。称\(\mathcal{H}(x_1, x_2,..,x_N) = \{ dichotomies\}\)。 比如上面举的例子中，三个输入情况下: \(\mathcal{H}(x_1, x_2, x_3) = \{ ooo, oox, oxo, oxx, xxx, xxo, xox, xoo\}\) 。
Growth Funciton 成长函数
我们发现\(\mathcal{H}(x_1, x_2,..,x_N)\)是跟\(x_1, x_2, ..x_N\)相关的，因此为了去掉这一个影响因素，基于Dichotomies, 我们定义成长函数: \[ m_{\mathcal{H}} = max(| \mathcal{H}(x_1, x_2, ..., )|), x_1, x_2...x_N \in \chi\]
很明显，它是关于\(N, \mathcal{H}\)的函数，我们计算下在上述的例子中的成长函数的值:
| N | \(m_{\mathcal{H}}(N)\) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | max(6,8) = 8 |
| 4 | 14 < \(2^4\) |
下面举几个不同的\(\mathcal{H}\)的成长函数。
1.Positive Rays: \(h(x) = sign(x-a)\), 输入空间为一维向量， 当\(x_i \geq a\), 输出 +1, 当\(x_i < a\) 时， 输出 -1. 如下: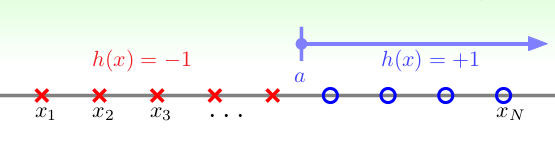 
可以发现，对于N个的输入，一共可以产生N+1个dichotomies, 就相当在N个位置中找一个位置作为a,然后加上一个边界，所以一共有N+1种.即: \(m_{\mathcal{H}}(N) = N + 1\)
2.Positive Intervals: 其实就是上一个的双向版， 输入空间仍为一维向量，当 \(x_i \in [l ,r] , y_i = 1; x_i \in [l, r], y_i = -1\), 如下: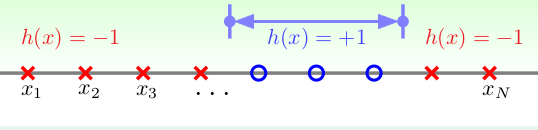 
根据1,可以很容易发现，这个的实质就是在N+1个位置，找两个位置，作为左右边界。所以\(m_{\mathcal{H}} (N) = \lgroup \begin{matrix} N+1 \\ 2 \end{matrix} \rgroup+ 1 = \frac{1}{2}N_2 + \frac{1}{2}N+1\),最后仍然会多一个dichotomies,就是l,r重合。
3.Convex Sets: 凸集合，如下图，其中 $R^2 $, 当 \(x_i\)在凸形内，\(h(x_i) = +1\), 反之则\(h(x_i) = -1\), 如下: 
这个\(\mathcal{H}\)的成长函数，也就是说最多有多少个dic，下面可以这样构造一\(\mathcal{D}\), 可以使得\(m_{\mathcal{H}}(N) = 2^N\),将所有的输入点在一个圆上，如下所示，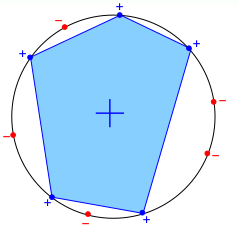 
这样我们可以随机选择k个点，然后这k个点组成的图形一定是凸的，在里面的点标为+1, 外面的标为-1。这样对于\(N\)个输入来说，任何一个组合都会是一个dictomies, 所以: \(m_{\mathcal{H}} = 2^N\).
break point & shatter
前面说了几个常见的成长函数:
- \(m_{\mathcal{H}}(N) = N+1\), Postive Rays
- \(m_{\mathcal{H}}(N) = \frac{1}{2}N_2 + \frac{1}{2}N+1\),Postive Inteervals
- \(m_{\mathcal{H}}(N) = 2^N\),convex sets
- \(m_{\mathcal{H}}(N) = 未知,\ 2D\ perceptron.\ m_{\mathcal{H}}(4) = 14 < 2^4\)
我们发现，除了 convex sets,其余的成长函数随着N的增大，都会小于\(2^N\),于是我们会猜想是不是会是多项式级别的呢？如果这样的话，用这个多项式替代最开始的M, 那么整个learning就解决了。
下面我们开始探讨成长函数的增长速度。随着N的增大，成长函数的值\(m_{\mathcal{H}}(N)\)第一次小于\(2^N\)的N的取值，我们称为 break point: 即 \[ \begin{align} m_{\mathcal{H}}(K-1) & = 2^N \\ m_{\mathcal{H}}(K) & < 2^K \\ \end{align} \]
我们称K为\(\mathcal{H}\)的break point.为什么要找K呢，因为我们想证明成长函数服从一个多项式的增长，而不是\(2^N\), 而第一个开始小于\(2^N\)的那个N，肯定需要着重考察。比如上面的几个例子里面:
- postive rays: $m_{}(N) = N + 1 = O(N), break-point: 2 $
- postive intervals: \(m_{\mathcal{H}}(N) = \frac{1}{2}N_2 + \frac{1}{2}N+1=O(N^2),\ break-point: 3\)
- convex sets: $m_{}(N) = 2^N, no break-point $
- 2D perceptrons: \(break-point : 4\)
基于break point,如果\(m_{\mathcal{H}}(N) = 2^N\),即当\(N < K\)时，我们称，\(\mathcal{H}\)把\(\mathcal{D}_N\)这N个input，shatter了。或者说，这N个输入被\(\mathcal{H}\) shatter 了，通俗一点就是说，我们的\(\mathcal{H}\)可以产生所有可能的输出。这几个概念在后续会一直用到。
总结
本节的主要提出了在M无穷的情况下，我们该如何处理，首先提出了使用\(h\)的类别来代替M, 然后只需要计算learning的\(h\)能够对\(\mathcal{D}\)分为有限类，那就开始的两个问题就明了了。比如如果我们证明，在 2D perceptrons中， \(m_{\mathcal{H}} = O(N-1)\), 那么根据 Hoeffdiing’s inequality:
\[P[ | E_{in} - E_{out} | > \epsilon ] \leq 2 \cdot effective(N) \cdot exp \lgroup -2 \epsilon^2N\rgroup\]
这里面的\(effective(N) = m_{\mathcal{H}} = O(N^{k-1})\) , 就说明我们的PLA 是正确的。后面开始证明\[m_{\mathcal{H}} = O(N^{k-1})\]