整理自台大林轩田老师的机器学习基石在线课程，以及参考了beader的文章，作为笔记。
一些机器学习入门的书籍大部分都是直接讲模型，却没有来龙去脉，感觉很虚。而林老师的第一部分是机器学习的基石，就是背后的东西，并没有直接去讲各种模型, 在第二部分机器学习技法才开始介绍模型。
课程前三节主要介绍了机器学习的一些基本概念(未知函数f, 学习算法A, 假设空间H等等)，以及讲了一个最简单的线性分类器: 感知器模型(PLA). 相对简单，比较容易接受。 这节开始主要介绍一些算法背后的理论，比如为什么机器学习为什么可行，以及为什么训练数据集越大，训练结果就越好。
learning的概览
learning的流程图: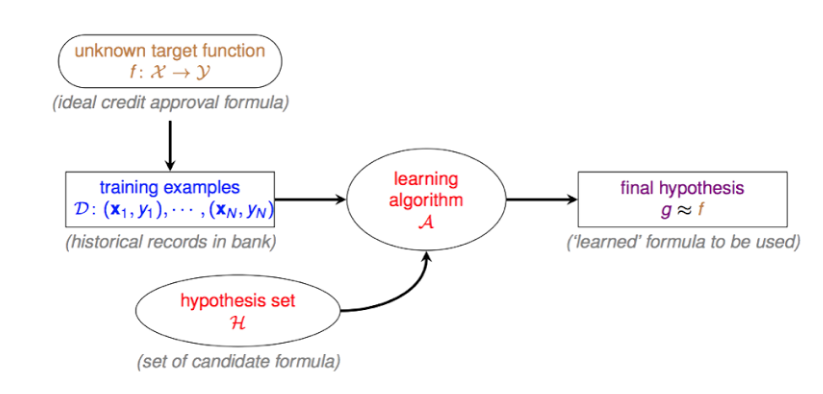 
下面仔细说明每个符号代表的意义: 当时看的时候，没搞透彻这几个符号，后面就很费劲了。
- \(\mathcal{f}: \chi \to \gamma\)
- \(\chi\) 表示输入空间，里面包含了很多组输入数据\(x_i\). 比如拿信用卡审核的例子来说，输入空间\(\chi\)可以是 (age, gender, annual salary, year in residence, year in job, current debt) 表示的六维的输入空间. (23, male, 10000,1,0.5, 20000)可能就是一组输入的数据。
- \(\gamma\) 则代表的是输出空间。比如前面提到的PLA的输出空间是\(\{+1, -1\}^1\), 在信用卡例子中，可以用+1表示未来会违约，-1表示未来不会违约。
- \(f\) 是很核心的概念，表示现实中未知的某个规律或者某个函数， 我们只能知道的是，把训练数据\(\mathcal{D}\)中的数据\(x_i\)作为输入，它会输出 \(y_i\).正因为它的未知，learning要做的事情就是找到一个函数\(\mathcal{g}\)能构接近\(\mathcal{f}\).接近的意思是指，\(\mathcal{g}\)对于训练数据\(\mathcal{D}\)中的运行情况与\(\mathcal{f}\)的运行情况类似。
- \(\mathcal{D}: {(x_1, y_1), (x_2, y_2),..., (x_N, y_N)}\)： 表示由输入空间\(\chi\)中的\(x\)以及输出空间\(gamma\)中的\(y\)组成的N条数据的训练数据集。
- \(\mathcal{H}\): 表示假设空间，也就是一堆函数的集合:\(\{ h_1, h_2, ...\}\)，我们要找的\(\mathcal{g}\)就在这里面寻找。
- \(\mathcal{A}\)：学习算法，通过\(\mathcal{A}\)，我们才可以在\(\mathcal{H}\)中找到最接近\(f\)的那个\(h\). 因为\(\mathcal{H}\)的数量是未知的，因此我们必须把学习算法设计的合适，才可以高效的找到那个\(h\)。
- \(\mathcal{g}\)：这个就是我们最后找到的hypothsis,就是通过学习算法\(\mathcal{A}\)找到的那个最接近f的函数。
有几个注意的点:
- \(\mathcal{D}\)是一个训练数据集，后面会区分多个训练数据集。
- \(f\) 一定是未知。learning的过程就是在\(\mathcal{H}\)里面找到在训练数据集\(\mathcal{D}\)表现接近f的那个hypothesis.
那么问题来了，假设我们找到了那个\(g\), 它在训练数据集上表现不错，但是在\(\mathcal{D}\)之外的其它数据表现也会跟\(f\)很接近吗？ 我们关心的不是它在训练数据集上表现多好，而是在未知数据集上的结果是不是很好，那么如果一个hypothesis在训练数据集上接近f，那么是不是在测试数据上跟f也差不多呢。这就是检验learning是不是真正学到了东西。
learning是否可行?（Feasibility）
learning是 impossible?
我们经验上感觉g如果在\(\mathcal{D}\)上的表现好的话， 那么它就是一个好的hypothesis。但是事实是这样吗？有这么一个二分类的简单例子：看训练数据如下： 
其中\(\chi \in \{ 0, 1\}^3, \gamma \in \{ o, X\}^1\).
举着个例子是因为很简单， 所有的数据以及\(\mathcal{H}\)里面所有的\(h\)都可以列举出来，如下: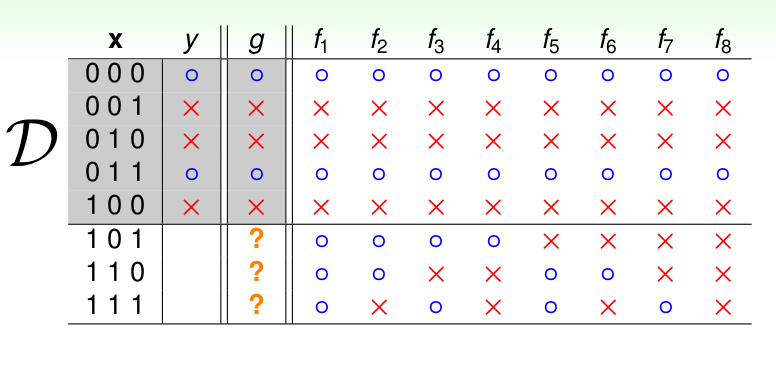 
我们发现8个\(h\) 在\(\mathcal{D}\)上都等于 \(f\). 但是在\(\mathcal{D}\)之外，却各不相同，那么我们应该选择那个作为我们最终的\(g\)呢？这里看来，好像机器学习并不能学到东西，我们好像并不能保证在训练数据集之外\(g\)是否还能跟\(f\)很接近。 这个问题需要后面解释
Inferring Something Unknown与统计结合
我们在统计里面知道抽样的概念，使用样本估计总体，比如样本均值估计总体期望， 或者用样本构造一些统计量来估计总体分布的参数。 比如下面的摸球的例子，一个罐子里面有橙色的球和绿色的球，但是不知道各自所占的比例。这时候我们呢经常采用抽样的方式，在罐子中抽出N个球，看看橙色和绿色占的比例，依次作为总体的概率。 如下: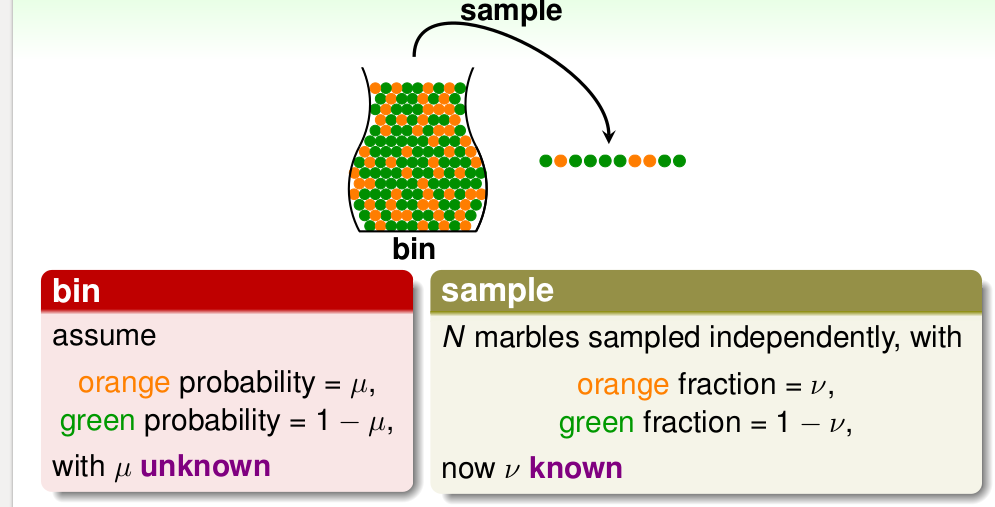 
那我们可不可以使用 样本中的\(\nu\)来代替总体中的\(\mu\)呢？ 似乎可以，但是好像仍有风险， 比如总体中，橙色，绿色占比例差不多，但是碰巧有一个Sample抽了10个都是绿色的(后面提到的BadData) ， 那这个时候，我们不能使用\(\nu\)代替 \(mu\), 不过经验还告诉我们好像10个都是绿色的发生概率并不是很大，尤其是随着样本数目的增加。 在统计中的Hoeffdiing's inequality 给出了具体的计算公式: \[P[\| \nu - \mu \| > \epsilon] \leq 2 exp \lgroup -2 \epsilon ^2 N \rgroup \]
称式子中的\(\epsilon\) 是允许误差的容忍度， 我们可以看到就是说 \(\nu\)与\(\mu\)的差距由\(\epsilon, N\) 控制的。当\(N\)变大的时候，\(\mu, \nu\)的差距的上限会降低。当\(\mu, \nu\)的差距小到一定程度了， 可以说它俩是差不多一样(PAC, probably approximately correct)。
以上是基于统计的观点，使用样本估计总体。 那该怎么与我们的 learning 对应起来呢？我们假设那一罐子球是假设空间\(\chi\), 对于某个hypothesis h，开始抽样，作如下对应:
- \(h(x_i) \neq f(x_i)\) 时， 对应球是橙色
- $h(x_i) = f(x_i) $时， 对应球是绿色
有了这个对应之后，样本中橙色球的概率\(\nu\)就是当前hypothesis的错误率\(error\)。 总体中的橙色球概率\(\mu\)则是\(h\)在总体分布下的错误率。这里我们定义两个新的变量:
- \(E_{in}(h) = \frac{1}{N} \sum_{n=1}^{N} \lVert h(x_n) \neq f(x_n) \rVert\), IN-SAMPLE-ERROR，h在训练集的错误率
- \(E_{out}(h) = \epsilon_{x \sim P} \lVert h(x) \neq f(x) \rVert\), OUT-SAMPLE-ERROR,在总体中\(h\)的错误率
很容易可以知道: \[ \begin{align} \mu &= E_{out}\\ \nu &= E_{in} \end{align} \]
代入Hoeffdiing's inequality 可以得到:
\[P[\| E_{in} - E_{out} \| > \epsilon] \leq 2 exp \lgroup -2 \epsilon ^2 N \rgroup\]
这就意味着，在不等式的上限在足够小的情况下，我们貌似可以说，\(E_{in}\)和\(E_{out}\) 达到了 PAC, 也就是说 h 在训练集中的表现与在总体中的表现接近，即：用已知的\(E_{in}\)去推断未知的\(E_{out}\) 。 但现在还不可以说，\(h\)是一个好的learning， 因为我们的目的不是\(h\), 而是一个接近\(f\)的\(g\), 因此我们需要的不仅仅\(E_{in}\)与\(E_{out}\)接近，更需要他们尽可能小，这样才是一个最好的最接近真理\(f\)的\(h\)。
Bad Data 坏数据
前面说了，使用某个训练集或者说抽样的样本，然后找一个\(E_{in}\)尽可能小的\(h\), 作为我们的\(g\). 但是如果训练数据集有问题呢？尤其是当N小的时候，误差是不可避免的，或者说噪音数据集。比如说想知道硬币朝上的概率，然后连续扔了5次，都出现了正面，这种情况下，显然不能说硬币朝上的概率是1吧。因为这样的样本本身是有误差的，对于整体 来说: \(E_{in} = 0; E_{out} = \frac{1}{2}\).这样使\(E_{in}\) 和 \(E_{out}\)差别很大的样本就称为BAD SAMPLE 说到learning, 对于某个 \(h\), 如果某个\(\mathcal{D}\)使得 \(E_{in}(h)\)与\(E_{out}(h)\) 差别很大，比如说\(E_{in}(h)\)很小，也就说在训练数据中表现很好，结果我们的算法\(\mathcal{A}\)就选择了它， 但是没想到\(\mathcal{D}\)之外的数据表现很差，\(E_{out}(h)\)很大， 这样就称这个\(\mathcal{D}\)对\(h\)来说是BAD DATA, 它会使得 \(\|E_{in} - E_{out}\| > \epsilon\)。那是不是机器学习啥也没学到呢？ 白忙活了？ 很显然，我们不希望遇见BAD DATA, 它对我们的learning很不好，那么出现BAD DATA的概率有多大呢？ 首先只要某个\(\mathcal{D}_i\) 对 \(h(h \in \mathcal{H})\) 是BAD DATA, 那么就称该\(\mathcal{D}\)是BAD DATA, 如下
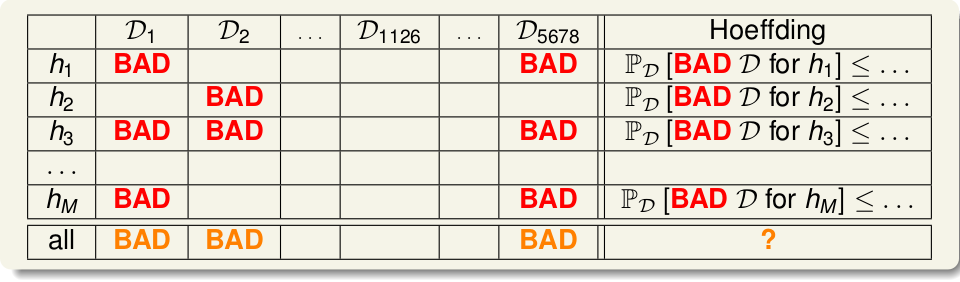
那我们就需要计算: 
其中\(M = \| \mathcal{H} \|\), 从式子中我们可以看出，遇到BAD DATA的概率的上限 与\(N, M, \epsilon\)有关。 因而也可以看出如果训练数据N越大，也就更不容易遇见BAD DATA, 对应到硬币则是，连续投硬币10次均出现正面的概率 小于 连续投5次。同理如果 M 越小，BAD DATA概率越小。
总结
说完了\(P[\| E_{in}(h) - E_{out}(h) \| > \epsilon] \leq 2 exp \lgroup -2 \epsilon ^2 N \rgroup\)， 我们知道\(E_{in}(h)\)与\(E_{out}(h)\)可以很接近,我们就可以大胆的选择\(E_{in}\)最小的\(h\)来作为我们的\(g\)。但是BAD DATA又告诉我们群众里面有坏人，如果遇到了，那么会影响我们的\(\mathcal{A}\) 挑选\(h\). 幸好，Hoeffding's Inequality 告诉我们 出现 BAD DATA的概率有个bound。 所以我们只要控制了BAD DATA出现的几率，还可以继续选择最小的\(E_{in}(h)\)了。 不过还有问题，\(M\) 如果很大了，比如在PAL中，\(\mathcal{H}\) 就是无穷多的直线，这时候，Hoeffding's Inequality貌似也不能起作用了，这就是后面要讨论的问题了: 当\(\| \mathcal{H} \| \to infty\)，我们该怎么办。