上节介绍的Kernel SVM的结尾,提到了overfit的问题,那是因为SVM要找到的分类面是必须把所有的训练数据分开,即使有一些噪音数据,或者说是错误标注的数据,也要"坚持"分开,这可能就会形成很复杂的边界,很容易形成overfit,如下:

我们希望的是左边的分类面,而非右边的,虽然右边的\(E_{in} = 0\),也就是说希望对于一些错误的数据忽略掉,前面介绍PLA的变种Pocket的用的就是这种方式:

Pocket找的是分类错误点尽可能少的分类面,不一定必须完全分开,容许错误的发生。而我们之前的SVM均是要求所有的数据都必须分类正确,如果我们将Pocket与SVM结合,即允许发生错误,如下:
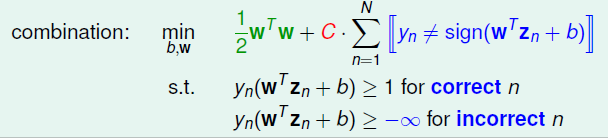
上式约束条件中,对于分类正确的点,仍然需要满足\(\geq 1\)的条件,对于当前分类错误的点不加任何限制。所以目标函数中除了原先的margin,还必须加入了分类错误的个数,对整体做最小化。系数\(C\)的作用则是一种对margin和犯错个数的一个折中。\(C\)越大表示犯错误越少越好,犯错误个数重要性大于margin,如果太大了, 就容易过拟合了,反之\(C\)越小表示希望magin 越宽越好,也就是说\(\mathbf{w}\)越小越好,就是说对错误的惩罚很小,这样就会导致分类效果变差。 用\(C\)表示更重视\(margin\)还是重视犯错误的多少, 如下图:
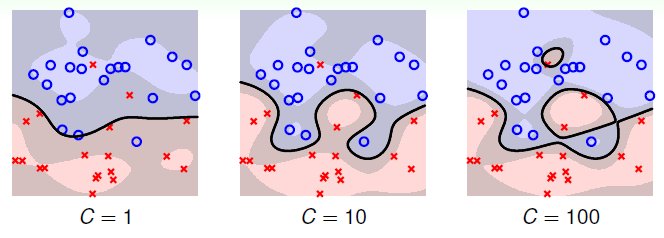
对于新的优化问题。然而由于存在bool的运算\(\neq\),也就是说该问题是离散的,无法用二次规划QP来求解。此外,还有一个缺点,那就是对所有的错误都是一视同仁的,无论是距离边界近还是远,只要分类错误,都计算在内,也就是说无法区分大错小错。
为了解决上述问题,引入变量\(\xi \geq 0\) 表示不满足\(y_n(\mathbf{w}^T\mathbf{z}+b) \geq 1\)的数据距离当前分类边界的距离,用来量化偏离的程度,也就是错误的大小,把原问题转为如下:
\[\begin{align} \min\limits_{b,\mathbf{w},\xi} & \quad \frac{1}{2}\mathbf{w}^T\mathbf{w}+C \cdot \sum\limits_{n=1}^N \xi_n \\ s.t. & \quad y_n(\mathbf{w}^T{\mathbf{z}}_n+b) \geq 1 - \xi_n, for \ all \ n; \\ & \quad \xi_n \geq 0, for \ all \ n\end{align}\]
对于满足margin条件的点其\(\xi =0\), 不满足margin条件的其\(\xi > 0\); 如下图:

图中有除了A,B两点之外的点均满足条件,\(\xi=0\); 而A点属于没有不满足margin条件的,B点属于分类错误,因此\(\xi_{A} >0, \xi_B>0\)。
上述的优化问题已经可以使用二次规划问题的解法去求解了,三个自变量:\(b,\mathbf{w},\xi\),一共有\(\tilde{d}+1+N\)维;约束条件的个数为\(2N\)个,按照前面的解法即可。
我们把这种容许犯错的SVM成为Soft-Margin SVM(软间隔SVM),与前面几节的Hard-Margin SVM相对,并且引入的\(\xi\)也叫做 松弛变量,顾名思义,允许数据偏离margin, 例如出现上图中A,B那样的数据。
上述的优化问题是Soft-Margin原始问题,下面考虑Soft-Margin的对偶问题(Dual),同Hard-Margin,只需将两个约束条件加入到Lagrange Function:
\[\begin{align}\mathcal{L}(b, \mathbf{w}, \xi, \alpha, \beta) = &\frac{1}{2}\mathbf{w}^T\mathbf{w}+C \cdot \sum\limits_{n=1}^N \xi_n \\&+ \sum\limits_{n=1}^{N}\alpha_n(1-\xi_n-y_n(\mathbf{w}^T\mathbf{z}_n+b)) \\ & +\sum\limits_{n=1}^{N}\beta_n(-\xi_n) \end{align} \]
然后将原始问题转为如下的对偶问题:
\[\max\limits_{\alpha_n \geq 0,\ \beta \geq 0}\left(\min\limits_{b, \mathbf{w}, \xi} \quad \mathcal{L(b, \mathbf{w}, \xi, \alpha, \beta)}\right)\]
优化思路同Hard-Margin的对偶问题相同,首先对内层最小化部分对变量求微分: \[\begin{align}& \frac{\partial \mathcal{L}}{\partial \xi_n} = C - \alpha_n - \beta_n = 0 \\ & \Rightarrow \beta_n=C-\alpha_n \end{align}\]
这样利用这个条件,就可以向Hard-Margin消去\(b\)一样去掉\(\beta_n\), 同时结合\(\beta_n \geq 0\)可以得到$ 0 _n C$。
整理一下式子,提取出\(\xi\)的部分:\(\sum(C-\alpha_n-\beta_n) \xi_n\),已知最优解满足\(\alpha_n+\beta_n =C\), 因此\(\xi\)部分可以消去,最终如下:
\[\max\limits_{ 0 \leq \alpha_n \leq C}\left(\min\limits_{b, \mathbf{w}} \quad \frac{1}{2}\mathbf{w}^T{\mathbf{w}} + \sum\limits_{n=1}^{N}\alpha_n(1-y_n(\mathbf{w}^T\mathbf{z}+b))\right)\]
除了外层的\(\alpha_n\)多了一个上限之外,与Hard-Margin的对偶问题完全一样,接下来对\(b, \mathbf{w}\)分别求微分,然后去掉\(b,\mathbf{w}\),再将外层最大化稍微化简,最终转为如下的二次规划(QP)问题:(此过程与Dual SVM中完全一样,不再重写一遍):
\[\begin{align} \min\limits_{\alpha} & \quad \frac{1}{2}\sum\limits_{n=1}^N\sum\limits_{m=1}^N \alpha_n\alpha_my_ny_m\mathbf{z}_n^T\mathbf{z}_m - \sum\limits_{n=1}^{N}\alpha_n \\ s.t. & \quad \sum\limits_{n=1}^{N}\alpha_ny_n = 0; \\ & \quad 0 \leq \alpha_n \leq C, \ n = 1,2...N \end{align}\]
当然还有一些中间条件: \(\mathbf{w} = \sum \alpha_ny_n\mathbf{z}_n, \beta_n=C-\alpha_n\);
到这里我们的问题转为了有\(N\)个变量,\(2N+1\)个约束条件的二次规划问题,表示出\(Q,p,A,c\)然后使用某个QP Solver即可得到最优的\(\alpha\):

- Q矩阵元素: \(q_{n,m} = y_ny_m\mathbf{z}_n^T\mathbf{z}_m\)
- $ p = -_N$
- 对于\(A,c\),对应如下:
- \(a_{\geq} = y, c_{\geq} = 0\)
- \(a_{\leq} = -y, c_{\leq} = 0\)
- 对于\(\alpha \geq 0\) 有\(a_n^T =\) n-th unit dircection, $c_n = 0 $
- 对于\(\alpha \leq C\) 有\(a_n^T =\) n-th unit direction, \(c_n = -C\)
到此为止,我们得到了对偶问题的最优的\(\alpha\), 再结合上节的Kernel Trick, 我们得到了 Kernel Soft-Margin SVM,基本流程如下:

这里有一点不一样的地方是对\(b\)的求解,回想之前是利用转化为拉格朗日对偶问题(min(max) \(\Leftrightarrow\) max(min))时候,利用互补条件(complementary slackness),参考Dual SVM, 但是Soft-Margin有两个条件,即:
\[\begin{align} \alpha_n(1-\xi_n-y_n(\mathbf{w}^T\mathbf{z}_n+b)) &=0 \\ \beta_n \xi_n = (C- \alpha_n)\xi_n & =0\end{align}\]
首先对第一个式子,对于SV(\(\alpha_s > 0\)), 那么可以得到 \(b=y_s - y_s\xi_s - \mathbf{w}^T\mathbf{z}_s\),但是里面含有\(\xi\),无法求解。 再看第二个式子,对于\(\alpha_s < C\)的那部分SV(也叫free SV),则有\(\xi_s = 0\),因此利用这部分SV, 加上Kernel Function便可得到\(b\):
\[b=y_s - \mathbf{w}^T\mathbf{z}_s = y_s - \sum\limits_{free \ SV} \alpha_ny_nK(\mathbf{x}_n, \mathbf{x}_s)\]
到这里基本完成了Soft-Margin SVM的算法,集对偶,核,Soft-Margin于一身,可以解决非线性问题,松弛变量允许噪音数据等,在实际分类问题中,应用很广泛。 不过需要注意的是这种SVM也有可能overfit的,因此需要仔细调整参数\(C\),以及Kernel Function的参数,一般使用模型验证(Validation)手段比如交叉验证去选择最好的参数。
最后再提一下Soft-Margin 中的\(\alpha\)的物理意义,看下图:

根据两个互补条件,可以得到三类点点:
- 非SV(支撑向量): 也就是距离分离面比较远的那些数据,如图中的圈圈叉叉,对应的\(\alpha_n = 0, \xi_n = 0\)
- free SV: 也就是说\(\alpha_n < C, \xi_n =0\),它们在边界上, 满足条件。图中方框标记的点,我们使用这些点计算的\(b\)。
- bounded SV: \(\alpha_n =C, \xi_n > 0\),这种类型的数据,不满足margin条件,或者分错类别的,如图中三角标记的。