这一节是核模型的最后一部分了,将Kernel引入到一般的回归模型中: 核岭回归(Kernel Ridge Regression)以及支持向量回归(Support Vector Regression),此外文末对这一占了整个课程40%的大块内容做了简单总结。
核岭回归
上一节的表示定理(Representer Theorem)说明,任何\(L_2\)正则化的线性模型的最优解都可以表示成数据的线性组合,也就可以引入Kernel了,进而更加Powerful。现在看之前的岭回归(\(L_2\)正则化的线性回归):
\[\min_{\mathbf w} \quad {\lambda\over N}\mathbf w^T\mathbf w+{1\over N}\sum_{n=1}^N\left(y_n-\mathbf w^T\mathbf z_n\right)^2\]
显然最优解\(\mathbf w_{*} = \sum \beta_n \mathbf z_n\),那么完全按照上一节KLR的形式,引入Kernel Function,用\(\beta\)替换\(\mathbf w\):
\[\begin{align} & \min_\beta \quad {\lambda\over N}\sum_{n=1}^N\sum_{m=1}^N\beta_n\beta_mK(\mathbf x_n,\mathbf x_m)+{1\over N}\sum_{n=1}^N\left(y_n-\sum_{n=1}^N\beta_mK(\mathbf x_n,\mathbf x_m)\right)^2 \\ \Leftrightarrow & \min_\beta \quad {\lambda \over N } \beta^TK\beta +{1 \over N} \left( \mathbf y^T \mathbf y - 2\beta^TK^T\mathbf y + \beta^TK^TK\beta\right)\end{align}\]
用矩阵表示一来看起来简介,求微分简单,二来矩阵计算比循环要快很多。(PS: 每一个\(\sum\)都可以表示为矩阵的乘积,如果一眼看不出来,就展开只能一点点的凑)。
同样得到一个这个无约束的优化问题了, 可以用梯度方式来直接接线性方程(KLR则需要梯度下降来求):
\[{\partial E_{in} \over \partial \beta} = {2 \over N}\left( \lambda K^TI\beta+K^TK\beta - K^T\mathbf y \right)\]
(引入\(I\)是为了后面与\(\lambda\)计算方便)然后令微分为0,得到下面的结果:
\[\beta = (\lambda I +K)^{-1}\mathbf y\]
前面在介绍SVM的时候提到过核函数矩阵K是半正定对称方阵,因此逆矩阵一定存在,对于\(N \times N\)的矩阵求逆矩阵复杂大是\(O(N^3)\),而且由于核函数矩阵大部分都不为0,最后得到的\(\beta\)也是非稀疏矩阵,因此在数据量比较大的时候,计算量还是蛮大的。
到此,上述的模型就称为: Kernel Ridge Regression,完整如下为:
\[g(\mathbf x) = \sum\limits_{n=1}^{N}\beta_nK(\mathbf x_n, \mathbf x)\]
通过引入核,可以解决非线性的回归预测问题了。下面对比带核与否的Ridge Regression的一些区别:

两种模型的优缺点与适用场合也就很明显了,只要数据量没有远大于数据维度的话,就可以用kernel ridge regression, 不过还是有一个原则: Linear First。
支持向量回归
上面的核岭回归由于核函数矩阵不稀疏,计算量比较大。而之前SVM则只考虑少部分的Support Vectors,得到的\(\alpha\)是sparse的,这一节就从Soft-Margin的角度来重新设计Linear Regression的误差衡量。
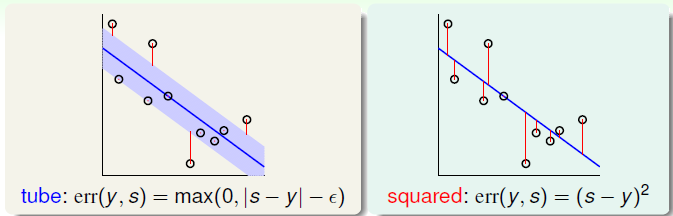
定义Tube Regression的误差为:
\[err(y,s)=\max(0, |s-y|-\epsilon), \quad s=\mathbf w^Tz_n +b, \ \epsilon > 0\]
也就是说,同Soft-Margin SVM分类问题容许偏差的存在,如果预测值与实际值的差距小于\(\epsilon\)的时候,就认为err=0,tube可以理解为预测误差在允许范围内,如下图对比tube error与 square error:
仿照SVM,加上\(L_2\)正则项的Tube Regression的目标函数定义为:
\[\min\limits_{b,\mathbf w}\left({1\over 2}\mathbf w^T\mathbf w+C\sum_{n=1}^N\max\left(0, \left\lvert \mathbf w^T\mathbf z_n+b-y_n\right\rvert-\epsilon\right)\right)\]
不过由于含有max项,无法微分因此求解很困难,我们可以参考在SVM的方法将问题转为二次规划问题来解决。下面引入新的松弛变量\(\xi_n \geq 0\)表示第n个数据的误差,这样目标函数转化为:
\[\begin{align} \min\limits_{b,\mathbf w} \quad &\left({1\over 2}\mathbf w^T\mathbf w+C\sum_{n=1}^N\xi_n)\right) \\ s.t. \quad & \left\lvert \mathbf w^T\mathbf z_n+b-y_n\right\rvert \leq\epsilon+\xi_n \\ &for \ all \ n, \xi_n \geq 0 \end{align}\]
这样的话,对于误差不大于\(\epsilon\)的数据,\(\xi_n=0\),反之则\(\xi_n > 0\),不过到此为止,还是不够的,因为约束条件里面有绝对值,这个还是无法用二次规划求解的。下面去掉绝对值,根绝取值的正负分两种情况,把\(\xi_n\)拆成两个个\(\xi_n^{\wedge}, \xi_n^{\vee}\),分别真实值大于模型得到的值,以及真实值小于模型得到的值的情形,得到的最终目标函数:
\[\begin{align} \min\limits_{b,\mathbf w} \quad &\left({1\over 2}\mathbf w^T\mathbf w+C\sum_{n=1}^N(\xi_n^{\vee}+\xi_n^{\wedge})\right) \\ s.t. \quad & \mathbf y_n-\mathbf w^T\mathbf z_n-b \leq\epsilon+\xi_n^{\wedge} \ \ \ \quad (1) \\ & \mathbf y_n-\mathbf w^T\mathbf z_n-b \geq -\epsilon-\xi_n^{\vee} \quad (2)\\&\xi_n^{\wedge}, \xi_n^{\vee} \geq 0 \end{align}\]
当真实值大于模型值的时候,需要满足约束条件(1),当真实值小于模型值的时候,需要满足约束条件(2),这样就是一个标准的二次规划的问题了。
到此为止,支持向量回归的原始问题(SVR Primal)就得到了,考察一下这个QP的规模: 一共有\(\tilde{d}+1+2N\)个变量(\(\mathbf w\)是Z-Space的权重,维度为\(\tilde{d}+1\)),\(2N+2N\)个约束条件,跟SVM的原始问题存在一样的缺陷,原始数据映射到Z-Space之后,维度太高,计算量过大。因此就引出了SVR Dual(支持向量回归的对偶问题)。
SVR Dual
对偶问题首先需要加入拉格朗日乘子,因为每个数据有四个约束条件,因此引入四个\(\alpha_n^{\wedge}, \alpha_n^{\vee},\beta_n^{\wedge}, \beta_n^{\vee}\geq0\):
\[\begin{align}\mathcal L(b, \mathbf w, \alpha^{\vee}, \alpha^{\wedge}) = &{1\over 2}\mathbf w^T \mathbf w+C\sum(\xi_n^{\vee}+\xi_n^{\wedge}) \\ +&\sum\alpha_n^{\wedge}(\mathbf y_n - \mathbf w^T\mathbf z_n -b-\epsilon-\xi_n^{\wedge}) \\+&\sum\alpha_n^{\vee}(-\epsilon-\xi_n^{\wedge}-\mathbf y_n + \mathbf w^T\mathbf z_n +b) \\+ & \sum\beta_n^{\wedge}(-\xi_n^{\wedge}) + \sum\beta_n^{\vee}(-\xi_n^{\vee})\end{align}\]
根据强对偶理论,以及在对偶SVM介绍的内容,Primal SVR 与下面的对偶问题等价:
\[\max \limits_{\alpha_n^{\vee}, \alpha_{n}^{\wedge}>0} \left( \min\limits_{b, \mathbf w, \epsilon} \mathcal L(b, \mathbf w, \xi^{\vee}, \xi^{\wedge})\right)\]
下面推导Dual SVR(课程中略):
首先求各个变量微分优化\(\min\):
\[\begin{align} &{ \partial \mathcal L \over \partial \xi_n^{\wedge}} = C-\alpha_n^{\wedge}-\beta_n^{\wedge} = 0 \quad \quad \quad \quad(1) \\ & {\partial \mathcal L \over \partial \xi_n^{\vee}} = C-\alpha_n^{\vee}-\beta_n^{\vee} = 0 \quad \quad \quad \quad (2)\\ &{\partial \mathcal L \over \partial b} = \sum(\alpha_n^{\vee}-\alpha_n^{\wedge}) = 0 \quad \quad \quad\quad (3)\\ & {\partial \mathcal L \over \partial \mathbf w } = \mathbf w - \sum(\alpha_n^{\wedge}- \alpha_n^{\vee})\mathbf z_n = 0 \quad(4)\end{align}\]
一共得到了4个(组)等式,这几个等式最优解也会满足,其中\(1 \leq\alpha_n \leq C\),将\(\beta^{\vee}, \beta^{\wedge}\),以及(3)式代入到\(\mathcal L\)中,消去\(\beta,b,\xi_n\),经过化简得到:
\[\begin{align}\min\limits_{\mathbf w} \mathcal{L}(b, \mathbf w, \xi_{\vee}, \xi^{\wedge}) &\Leftrightarrow \min \quad {1\over 2}\mathbf w^T\mathbf w + \sum(\alpha_n^{\vee}-\alpha_n^{\wedge})\mathbf w^T\mathbf z_n +\sum(\alpha_n^{\wedge}(y_n-\epsilon) + \alpha_n^{\vee}(-\epsilon-y_n) ) \\ &\Leftrightarrow \min \quad {1\over 2}\mathbf w^T\mathbf w -\mathbf w^T\mathbf w +\sum(\alpha_n^{\wedge}(y_n-\epsilon) + \alpha_n^{\vee}(-\epsilon-y_n) ) \\ &\Leftrightarrow -{1 \over 2}\sum\limits_{n=1}^N\sum\limits_{m=1}^N(\alpha_n^{\wedge}- \alpha_n^{\vee}) (\alpha_m^{\wedge}- \alpha_m^{\vee})K(\mathbf x_n, \mathbf x_m)\\ & \quad \quad +\sum(\alpha_n^{\wedge}(y_n-\epsilon) + \alpha_n^{\vee}(-\epsilon-y_n) ) \end{align}\]
上面的过程我们已经引入了核函数代替\(\mathbf {z_nz_m}\),至此最小化过程完成,开始考虑最外面\(\max\)部分,取相反数,结合约束来求最小值,最后的问题如下:
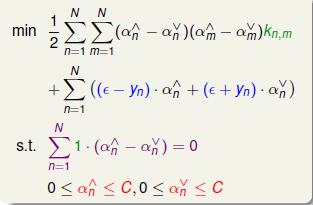
上式就是一个标准的二次规划问题,一共有\(2N\)个变量,按照格式写出QP Solver的Q,p,A,c,即可得到最优解\(\alpha_n^{\vee}, \alpha_n^{\wedge}\)。
最后返回到模型,在对偶问题中,我们还有一个很重要的互补条件(complementary slackness),如下:
\[\begin{align}\alpha_n^\wedge\left(\epsilon+\xi_n^\wedge-y_n+\mathbf w^T\mathbf z_n+b\right)&=0\\ \alpha_n^\vee\left(\epsilon+\xi_n^\vee+y_n-\mathbf w^T\mathbf z_n-b\right)&=0 \\ \beta_n^{\vee}\xi_n^{\vee}=(C-\alpha_n^{\vee})\xi_{n}^{\vee} &=0 \\ \beta_n^{\wedge}\xi_n^{\wedge}=(C-\alpha_n^{\wedge})\xi_{n}^{\wedge} &=0 \end{align}\]
现在考虑一些点: \(|\mathbf w^T\mathbf z_n +b - y_n| < \epsilon\),也就是那些在tube内部的,预测值与真实值的误差在允许范围内的点,对于它们,以下条件成立:
\[\begin{align} & \xi_n^{\vee} = \xi_n^{\wedge} = 0 \\ \Rightarrow &\epsilon -y_n+\mathbf w^T\mathbf z +b\neq0 \\ & \epsilon +y_n-\mathbf w^T\mathbf z -b\neq0 \\ \Rightarrow & \alpha_n^{\vee} =0 \\ & \alpha_n^{\wedge}=0 \end{align}\]
根据前面条件\(\mathbf w=\sum\limits_{n=1}^N(\alpha_n^{\wedge}-\alpha_n^{\vee})\mathbf z_n\),我们开始的目标之一便是想得到一个比较稀疏的系数, 现在对于在误差范围内的点\(\mathbf z_n\)的系数已经为0。只有在tube外面的数据点的不为0,这些点也就是Supports Vectors。
对于\(b\)的解法,同soft-margin SVM,从Support Vectors中考虑,只需要找到某个\(0<\alpha_s<C\)的数据,这样由互补约束便可知\(\xi_s=0\),从而得到b:
\[b = \epsilon + y_s -\mathbf w^T\mathbf z_s = \epsilon + y_s -\sum(\alpha_n^{\wedge}-\alpha_n^{\vee})K(\mathbf x_s, x_n)\]
最后得到Support Vector Regression(SVR)模型: \(g(\mathbf x)=\sum(\alpha_n^{\wedge}-\alpha_n^{\vee})K(\mathbf x_n, \mathbf x) + b\)
核模型(Kernel Model)总结
到此为止,线性模型/核模型这一大块的内容基本完结了,占了技法课程的40%。回顾一下,整理一下,有如下约10个模型或者算法那:
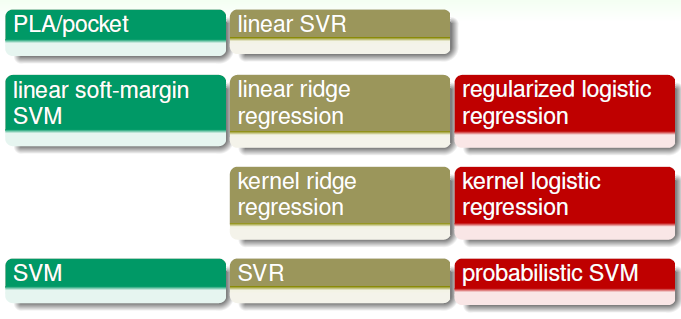
在实际中我们一般使用较少的有 PLA, Linear SVR,因为效果不好,限制很大。而至于Kernel Ridge Regression(核岭回归), Kernel Logistic Regression(核逻辑回归)也使用较少,因为其权重矩阵是稠密的(dense),计算量较大。相比核岭回归,在实际中更加倾向使用SVR; 相比核逻辑回归,更倾向于使用概率SVM。常用的一般有SVM, SVR, 线性岭回归,L2正则化的逻辑回归等。