接着上一节的Dual SVM,我们解决了非线性转换维度变高导致求解困难的问题,但是仍然有问题,那就是在求Q矩阵的时候,由于涉及到了高维的内积,计算量仍然很大,这一节引入核机制(Kernel Trick)来高效的求解这一过程,完全不再依赖高维空间。
核的引入
由上一节可以知道,计算量集中在Q矩阵中元素的计算:
\[\begin{align}q_{n,m} &= y_ny_m\mathbf{z}_n^T\mathbf{z}_m \\ &=y_ny_m\phi(\mathbf{x}_n)^T\phi(\mathbf{x}_m)\end{align}\]
这里分为两步,首先是空间转换,然后在高维空间中进行内积运算,这个计算量会很大的,尤其是后面还会有无穷维的转换,那么这一步根本无法完成。 如果我们将这两步合成一步的话, 就会降低计算量。下面以二阶多项式转换为例介绍: 假设原始数据有d维: \(\mathbf{x}=(x_1...x_d)\),
\[\phi_2(\mathbf{x}) =(1, x_1,x_2...,x_d, x_1^2,x_1x_2,...,x_1x_d,...,x_2x_1,x_2^2,...,x_d^2)\]
那么对两个数据\(\mathbf{x}, \mathbf{x}^{'}\)计算内积如下:
\[\begin{align}\phi_2(\mathbf{x})\phi_2(\mathbf{x}^{'}) &= 1 + \sum\limits_{i=1}^{d}x_ix_{i}^{'} + \sum\limits_{i=1}^{d}\sum\limits_{j=1}^{d}x_ix_jx_i^{'}x_j^{'} \\ &= 1 + \sum\limits_{i=1}^{d}x_ix_{i}^{'} + \sum\limits_{i=1}^{d}x_ix_i^{'}\sum\limits_{j=1}^{d}x_jx_j^{'} \\ &=1 + \mathbf{x}\mathbf{x}^{'} + (\mathbf{x}\mathbf{x}^{'})^2 \end{align}\]
可以发现,我们将转换与计算内积的过程转为了一步完成,就是上式,而且计算仅仅在原始维度上进行,复杂度从\(O(\tilde{d})\)降到了\(O(d)\),完全去除了对\(\tilde{d}\)的依赖。
我们称\(K_{\phi}(\mathbf{x},\mathbf{x}^{'}) = \phi_2(\mathbf{x})\phi_2(\mathbf{x}^{'})\)为核函数(Kernel Function)。比如\(K_{\phi_2} = 1 + \mathbf{x}\mathbf{x}^{'} + (\mathbf{x}\mathbf{x}^{'})^2\) 。核函数主要作用就会使得内积计算都在原始维度上,与高维空间无关,属于一种内积的运算简化技巧(Kernel Trick)。
有了核函数,我们便可以将Q矩阵改写如下:
\[q_{n,m} = y_ny_mK(x_n,x_m)\]
其余变量不变,求解新的二次规划问题,得到拉格朗日乘子\(\alpha\),由于我们跳过了转换过程,所以无法计算单独的\(\mathbf{z}\),因此利用\(\alpha\)求\(\mathbf{w},b\)的方法也得做一定修改。
先看\(b\),利用某个SV即\(\alpha_s >0\)来求:
\[\begin{align}b &= y_s - \mathbf{w}^T\mathbf{z}_s \\&=y_s - \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\mathbf{z}_s \\&=y_s - \sum\limits_{n=1}^{N}\alpha_ny_nK(\mathbf{x}_n, \mathbf{x}_s) \end{align}\]
这样就得到了\(b\)的表达式。
再看\(\mathbf{w} = \sum\alpha_ny_n\mathbf{z}_n\),貌似无法求解,因为这里面的\(\mathbf{z}_n\)没有办法求解。但是从另一个角度想,我们计算\(\mathbf{w}\)的目的就是为了计算\(\mathbf{w}^T\mathbf{z}\),那么我们整体计算看看得到什么:
\[\mathbf{w}^T\mathbf{z} = \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\mathbf{z} = \sum\limits_{n=1}^{N}\alpha_ny_nK(\mathbf{x}_n\mathbf{x} \]
这样也间接完成了我们的目的。这样利用Kernel Function,我们就避开了在高维空间的计算,甚至不需要知道用的什么映射,就直接在原始低维数据进行等价计算。
总结一下核机制SVM的一般流程:

再来看看每一步的复杂度,如下,第一步的\(O(N^2)\)是因为Q矩阵的规模是\(N*N\)的。

上面举的例子是二阶的核函数,下面介绍几个常用的核函数。
多项式核
我们将\(K_{\phi_2} = 1 + \mathbf{x}\mathbf{x}^{'} + (\mathbf{x}\mathbf{x}^{'})^2\) 加一些系数,得到更加简单更加常用的\(K_2(\mathbf{x},\mathbf{x}^{'})=(1+\gamma\mathbf{x}\mathbf{x}^{'})^2\),如下:

需要注意的是,\(K_2,K_{\phi_2}\)这两种核函数的能力本质上是相同的,也就是说解决同一类问题结果类似,只不过最后求出的边界不同。
此外,多项式核可以推向更一般的情况,如下:

其中\(\zeta,\gamma\)是超参数,\(Q\)是阶数。
这里面有一个特殊的: 线性核(Linear Kernel),计算简单高效:
\[K_1(\mathbf{x},\mathbf{x}^{'}) = (0 + 1 *\mathbf{x}\mathbf{x}^{'})^1 = \mathbf{x}\mathbf{x}^{'}, \quad \zeta=0, \gamma=1, Q=1\]
在实际应用中,还是需要遵循Linear First的原则,首先尝试Linear Kernel,高阶的核函数虽然能力强,但是相对容易造成OverfFitting。
高斯核
除了多项式核函数,另外常用的核函数还有高斯核函数,也叫做径向基函数(Radial Basis Function, RBF):
\[K(\mathbf{x},\mathbf{x}^{'}) = exp(-\gamma\Arrowvert \mathbf{x}-\mathbf{x}^{'}\Arrowvert^2), \quad \gamma >0\]
RBF核实现的是无限维的转换,证明思路就是将高斯核函数可以表示为无穷项的和,并且需要是两个向量内积的形式。下面以一维为例,即\(\mathbf{x}=(x_1)\),基于泰勒展开来证明:
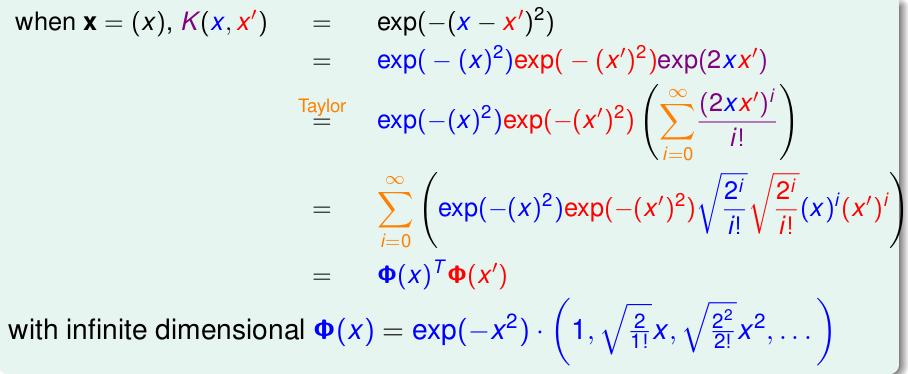
高斯核\(K(\mathbf{x},\mathbf{x}^{'}) = exp(-\gamma\Arrowvert \mathbf{x}-\mathbf{x}^{'}\Arrowvert^2), \quad \gamma >0\) 只有一个参数\(\gamma\),在实际应用中,\(\gamma\)一般不应该太大,否则很容易过拟合,还有一点高斯核完成的是到无穷维的转换,因此它的描述能力很强,可以作出很复杂的边界,但是由于是无穷维的转换,这个转换过程类似黑盒子,也就是说\(\mathbf{w}\)也是无穷维的,我们无法计算出它,因此也就缺乏了物理意义。
核比较
下面对线性核,多项式核,高斯核(RBF)做个对比。
线性核(Linear Kernel) \(K(\mathbf{x}, \mathbf{x}^{'}) = \mathbf{x}\mathbf{x}^{'}\):

- 优点: 泛化性能好,计算快速,应该优先考虑,解释性强,因为各个特征的重要性就直接体现在权重内。
- 缺点: 模型太简单,限制较大,比如线性不可分的数据
主要用于线性可分的情形,速度快,优先考虑。
多项式核(Ploy Kernel)
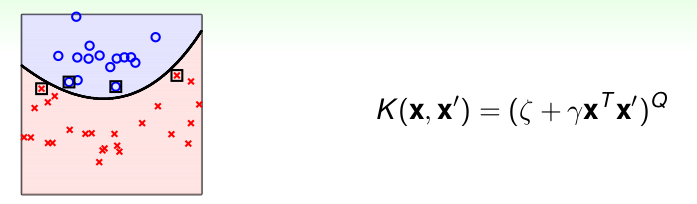
- 优点: 比线性核更加Powerful, 可以解决线性不可分的数据。
- 缺点: 超参数多(\(\zeta, \gamma, Q\)),不易选择; 另外 Q如果比较大的时候,矩阵的数值范围过大或者过小,不易计算,此外需要注意过拟合
一般使用的比较小的Q。 不过使用较少,因为速度不如Linear,能力不如RBF
高斯核(RBF Kernel)
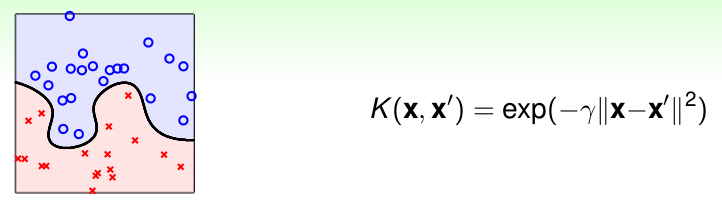
- 优点: 分类更加Powful,可以得到很复杂的边界,; 只有一参数\(\gamma\),模型选择更加简单。
- 缺点: 解释性差,因为无法计算无限维的\(w\),无法知道各个特征的权重; 过拟合更加严重,需要严格控制\(\gamma\)。
与Linear Kernel 一样,很常用,用于线性不可分的情形,参数多,因为计算量多,相对耗时较多。
总结
一般情况,使用线性核或者高斯核,RBF更加通用,参数好的话,基本会比Linear好,但是耗时多。
吴恩达NG教程中提到的以下经验:
- 如果Features数量大,与样本数量持平或者大于,这时候一般用Linear Kernal
- 如果Features较少,采用RBF Kernel
- 如果样本量过大的话,使用带Kernel的SVM优势就不大了。
最好的方式是根据具体数据来尝试哪种效果最好。
那么除了上述的Linear Kernel,Poly Kernel,RBF Kernel 之外,还有其它的核函数吗?
我们已经知道核函数是为了简化内积运算的trick,只知道\(K(\mathbf{x}, \mathbf{x}^{'}) = \phi(\mathbf{x})\phi(\mathbf{x}^{'})\),此外我们知道向量内积就是描述向量的相似度,(比如向量垂直,内积为0; 相反,内积为负数),那么我们能否从某个相似性出发,随意指定某个函数来作为相似度的描述?Not Really。Mercer Condition是用来判断一个函数能否作为核函数的条件。我们将数据写成核矩阵\(K\)的形式:\(K_{i,j} = K(\mathbf{x}_i, \mathbf{x}_j)\),整个矩阵如下:

很显然,K应该满足对称性,半正定的性质,事实上,对称,半正定也是K可以作为核矩阵的充要条件(证明略过),虽然可以指定某个函数作为核函数,但是在实际中,Linear Kernel和RBF Kernel已经足够用了。
后续
这一节主要介绍了 Kernel Trick SVM,首先引入核的概念,用来简化内积运算,再到几种常见核函数的优缺点的比较,最后稍微提了Mercer's Condition指出了作为核函数的充要条件。 到这里似乎SVM的分类问题貌似解决了,但是正如前面提到的,一直存在一个OverFitting的问题,比如说如果存在某些错误噪音数据,那么就算转到高维空间仍然存在线性不可分的情况,此时,就会产生很复杂的分类边界,造成OverFitting,但是我们更希望,忽略个别的错误数据,如下图:

这个问题就是下一节要解决的问题: Soft-Margin。