对偶SVM主要解决在非线性转换之后维度变高二次规划问题求解困难的问题。
在上一节的Linear SVM的最后提到了,在非线性分类问题中,我们一般作非线性转换\(\textbf{z}_n = \phi(\textbf{x}_n)\),从而在\(\textbf{z}\)空间里面进行线性分类,在非线性转换过程一般是一个升维的过程,将\(\textbf{z}\)的维度一般设为\(\tilde{d}\), 一般情况 \(\tilde{d} >> d\),(比如2维变5维,3维变19维等是一个非线性升高),这样在高维空间内部,在二次规划问题中的就会有\(\tilde{d}+1\)个变量,那么权值维度同样也为\(\tilde{d}+1\)维,以及\(N\)个约束,此外\(Q\) 矩阵维度会十分大,达到\(\tilde{d}^2\),因此,一旦\(\tilde{d}\)变大了, 二次规划问题求解就会变得很困难。
这一节就是通过引入对偶问题以及下一节的核,来消除SVM解决非线性问题转换到高维空间中对\(\tilde{d}\)依赖问题。
对偶的引入
我们的目标是将原始的非线性问题,转化为另外一个对等问题,使得新的对等问题的规模或者说复杂度(主要指二次规划问题的规模,比如变量数目,约束条件数目等)仅仅与原始数据的规模(样本量)有关,与转换的高维空间无关,如下:

拉格朗日函数
在引入对偶问题之前,在回顾上一节的二次规划问题SVM:
\[ \begin{align} & \min \limits_{b, \textbf{w}} \quad \frac{1}{2}\textbf{w}^T\textbf{w} \\& s.t. \quad y_n(\textbf{w}^T\textbf{x}+b) \geq 1 \end{align} \]
我们从另一个角度考虑,这里我们引入拉格朗日函数(Lagrange Function)来将约束条件和目标函数结合到一个式子:
\[\mathcal{L}(b, \textbf{w}, \mathbf{\alpha}) = \frac{1}{2}\textbf{w}^T \textbf{w} + \sum\limits_{n=1}^{N}\alpha_n(1-y_n(\mathbf{w}^T\mathbf{x}+b)), \quad \alpha_n \geq 0\]
其中\(\mathbf{\alpha}\) 为拉格朗日乘子(Lagrange Multiplier)。
下面我们将说明原始SVM二次规划问题与下式等价,即:
\[\mathbf{SVM} \equiv \min \limits_{b, \mathbf{w}} (\max \limits_{\alpha_n \geq 0} \mathcal{L}(b, \mathbf{w},\alpha))\]
首先右式表示多元变量的优化问题,首先在固定\(b,\mathbf{w}\)下,通过调整\(\alpha\),使得\(\mathcal{L}(b, \textbf{w}, \alpha)\) 最大,进而再优化外面的\(\min\)部分。
再看\(\max\)部分,分两种情况叙述:
- \(\mathbf{w},b\)不满足约束条件\(y_n(\mathbf{w}^Tx+b) \geq 1\),即: \(1-y_n(\mathbf{w}^T\textbf{x}+b) > 0\),再结合\(\alpha_n \geq 0\),很显然, \(\max(\mathcal{L}) \to \infty\)
- \(\mathbf{w},b\)满足\(1-y_n(\mathbf{w}^T\textbf{x}+b) \leq 0\),那么在求\(\max\)的时候,显然需要\(\alpha_n(1-y_n(\mathbf{\mathbf{w}^T\mathbf{x}+b})) = 0\),此时\(\max(\mathcal{L}) = \frac{1}{2}\textbf{w}^T \textbf{w}\)
显然,求完了\(\max\)之后,在优化外层求\(\min\)的时候,对于上述第一种\(\infty\)情况,肯定不会是最优解,因此最后的优化方程为: \(\min \frac{1}{2}\textbf{w}^T \textbf{w}\),因此与原始问题等价。这样,我们就把原始的含有约束条件的优化问题,转为不含条件的表达式。
对偶问题转化
接着化简,因为\(\max \geq any\),则对于任意一个给定的\(\alpha^{'}\),下式显然成立:
\[ \min \limits_{b, \mathbf{w}} (\max \limits_{\alpha_n \geq 0} \mathcal{L}(b, \mathbf{w},\alpha)) \geq \min\limits_{b, \mathbf{w}} \mathcal{L}(b, \mathbf{w},\alpha^{'})\]
既然上述的\(\alpha^{'}\)是任意给定的,那么左式也一定大于等于其中的那个最大的,那么下式也显然成立:
\[ \min \limits_{b, \mathbf{w}} (\max \limits_{\alpha_n \geq 0} \mathcal{L}(b, \mathbf{w},\alpha)) \geq \max\limits _{all \ \alpha_n \geq 0} (\min\limits_{b, \mathbf{w}} \mathcal{L}(b, \mathbf{w},\alpha^{'}))\]
到此为止: 观察上述不等式,最大化与最小化做了交换,这样的不等式,右式就称为左式的对偶问题,左式的下限就是右式。
此外,上述不等式关系属于一种弱对偶关系(Weak Duality)。如果满足下面的几个条件,则可以去掉不等号,从而转为强对偶关系(Strong Duality):
- 原始问题为是凸优化问题 (convex primal)
- 原始问题线性可分的(feasible primal)
- 约束条件是线性的(Linear constraints)
显然,原始问题满足以上强对偶条件,也就是说存在一组最优解\(\mathbf{w},b,\alpha\)同时满足式子两边。到此,我们将原始的问题转化为其如下的对偶问题:
\[\begin{align*}\max\limits_{all \ \alpha_n \geq 0}{\left ( \min\limits_{b,\mathbf{w}}{ \underbrace{\frac{1}{2}\mathbf{w}^T\mathbf{w}+\sum\limits_{n=1}^{N}\alpha_n(1-y_n(\mathbf{w}^T\mathbf{z}_n+b))}_{\mathcal{L}(b, \mathcal{w}, \alpha)}}\right)}\end{align*}\]
为什么要将原始问题,转换为对偶问题去求解呢?
开始说了, 目标是降低算法的规模或者说是复杂度。原始问题的最关于后需要解决的\(\min\limits_{b,\mathbf{w}}\)部分的复杂度是关于\(\mathbf{w}\)的,也就是高维空间的维度,求解很困难。而对偶问题最后要解决的\(\max\limits_{\alpha}\)则是关于\(\alpha_n\)的,复杂度跟样本数量\(N\)有关,在非线性分类中一般情况升维会达到很大的数量级(比如后续的高斯核是无穷维),远远大于样本数量,这个时候用对偶问题来求解就会容易。
此外,如果是线性分类且样本维度低于样本数量的话,那就直接使用原始问题求解即可,无需对偶。
求解对偶问题
最小化
固定\(\alpha\), 对拉格朗日函数\(\mathcal{L}\)最小化(凸函数),\(\mathcal{L}\)含有\(b, \mathbf{w}\)两个变量,因此分别求一阶微分:
首先对\(b\)求偏微分,得到:
\[\begin{align*} \frac{\partial\mathcal{L}(b, \mathbf{w}, \alpha)}{\partial \ b} = \sum\limits_{n=1}^{N}\alpha_ny_n = 0\end{align*}\]
因此我们最终得到的最优解应该满足上述条件,接着作一步转化:
\[\min\mathcal{L}(b, \mathbf{w},\alpha) = \min \frac{1}{2}\mathbf{w}^T\mathbf{w} + \sum\alpha_n(1-y_n\mathbf{w}^T\mathbf{z}^n) - {b*\sum\alpha_ny_n}\]
既然我们的最优解需要满足\(\sum\alpha_ny_n = 0\),那么上式也应该满足,那么蓝色部分就会变成0,问题得到了简化。
接着对\(\mathbf{w}\)求微分如下:
\[\begin{align*} \frac{\partial\mathcal{L}(b, \mathbf{w}, \alpha)}{\partial \ \mathbf{w}} = \mathbf{w} - \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n = \mathbf{0}\end{align*}\]
即最优解满足: \(\mathbf{w} = \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\),接着继续化简\(\min\mathcal{L}\):
\[\begin{align} \min\mathcal{L}(b, \mathbf{w},\alpha) & \Leftrightarrow \min \frac{1}{2}\mathbf{w}^T\mathbf{w} + \sum\alpha_n(1-y_n\mathbf{w}^T\mathbf{z}^n) \\ &\Leftrightarrow \min \frac{1}{2}\mathbf{w}^T\mathbf{w} - \sum \alpha_ny_n\mathbf{z}^n\mathbf{w}^T+ \sum\alpha_n \\ & \Leftrightarrow {\min} -\frac{1}{2}\mathbf{w}^T\mathbf{w} + \sum\limits_{n=1}^{N}\alpha_n \\ & \Leftrightarrow -\frac{1}{2} \Arrowvert \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\Arrowvert + \sum\limits_{n=1}^{N}\alpha_{n}\end{align} \]
经过分别求偏微分,并且将得到的条件代入到优化方程,最终去掉了\(\min\),仅仅与\(\alpha\)有关。
现在我们的问题化简至下式:
\[\begin{align*}\max\limits_{\alpha_n \geq 0, \ \sum\alpha_ny_n =0, \ \mathbf{w}=\sum\alpha_ny_n\mathbf{z}^n}\left( -\frac{1}{2}\Arrowvert\sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\Arrowvert^2+ \sum\limits_{n=1}^{N}\alpha_{n}\right)\end{align*}\]
至此最小化部分完成,完全转为了\(\alpha\)的问题。
最大化
上一步的最小化结束了,这一部分做外层的最大化,这里仅仅与\(\alpha\)有关。首先做一个转化,变为求\(\min\),然后展开平方如下:
\[\begin{align} \min\limits_{\alpha} & \quad \frac{1}{2}\sum\limits_{n=1}^{N}\sum\limits_{m=1}^{N}{\alpha_n\alpha_m} y_ny_m\mathbf{z}_n\mathbf{z}_m {-}\sum\limits_{n=1}^{N}\alpha_n \\ s.t. & \quad \alpha _n \geq 0, \ \sum\limits_{n=1}^{N}\alpha_ny_n =0 \end{align} \]
相当与将条件再提出来,就转化为QP问题求解!并且上式中\(N\)个变量\(\alpha_1...\alpha_N\),以及\(N+1\)个约束条件,这样就看着摆脱了高维,求解相对容易,这便得到就是标准SVM对偶问题。
下面便是根据QP问题的格式,写出对应的\(Q,p,A,c\):

这里需要说明一下:
- \(q_{m,n}\)表示矩阵\(Q\)的第\(m\)行第\(n\)列的元素
- 对于\(\sum y_n\alpha_n =0\),改为两个不等式条件: \(\sum y_n \alpha_n \leq 0,\ \sum y_n\alpha_n \geq 0\),因此一共有\(N+2\)个约束条件。
模型求解
利用QP Solver 就可以解决上述的二次规划问题,得到最优的\(\alpha=[\alpha_1...\alpha_N]\),下面介绍如何根据\(\alpha\)求解最优的\(\mathbf{w},b\),进而得到模型。
到这里整理一下已经有的条件:
- 对于原始问题有: \(y_n(\mathbf{w}^T\mathbf{z}_n+b) \geq 1\)
- 对于对偶问题有: \(\alpha_n \geq 0\)
- 对于对偶问题里层的\(\min\)优化求解中,有: \(\sum \alpha_ny_n =0; \ \mathbf{w}=\sum\alpha_ny_n\mathbf{z}_n\)
- 对于原始问题里层的\(\max\)问题中:上面得到结论有: \(\alpha_n(1-y_n(\mathbf{\mathbf{w}^T\mathbf{z}_n+b})) = 0\) ,被称为complementary slackness
注:上述条件即使二次规划问题中的 KKT条件(Karush-Kuhn-Tucker Conditions)
根据条件3,便可得到 \(\mathbf{w} = \sum\limits_{n=1}^{N}\alpha_ny_n\mathbf{z}_n\)。
根据条件4,我们知道\(\alpha_n\)以及\(1-y_n(\mathbf{w}^T\mathbf{z}_n + b)\) 至少有一个为0,我们只需要找到一个\(\alpha_n > 0\)的数据点,这样就会有:\(1-y_n(\mathbf{w}^T\mathbf{z}_n + b) = 0\),进而得到:
\[b = y_n - \mathbf{w}^T \mathbf{z}_n, \quad \alpha_n > 0\]
这里需要注意的是: \(\alpha_n > 0\)的点满足\(y_n(\mathbf{w}^T\mathbf{z}_n + b) = 1\),即分类边界上的点,也就是SV(Support Vector),这也就说明了 ,我们只需要SV就可以得到\(\mathbf{w},b\),这时候其它的点不需要。
简略总结一下标准对偶SVM的流程
- 根据训练数据,(非线性转换\(z_n = \phi(x_n)\), 写出QP问题的\(Q,p,a,c\)
- 使用QP Solover 求出最优的\(\alpha\)
- 根据条件约束,求出\(\mathbf{w},b\)
- 得到模型:\(g_{svm} = sign(\mathbf{w}^T\phi(\mathbf{x})+b)\)
数据表示模型
在开始介绍SVM的时候,就是以PLA为基础的,下面看看二者:
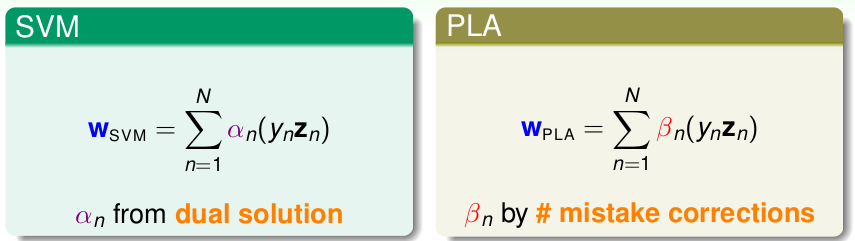
首先在Dual SVM中,\(\mathbf{w}\)是以\(y_n\mathbf{z}_n\)的线性组合求解的,其中参数为\(\alpha_n\); 在PLA中 同样,每个分类错误的点,都会加上\(y_n\mathbf{z}_n\),因此实质上\(\mathbf{w}\)同样线性组合求解得到。
其实还有很多线性模型或者算法,比如前面的Linear Regresson, Logistic Regression等如果初始化的\(\mathbf{w} = \mathbf{0}\),最终得到的最优解同样是数据的线性组合。
这个时候,我们就称参数w是被训练数据表示出来的(represented by data),只不过SVM的权重参数只需通过\(\alpha_n >0\)的SV表示即可。(PS:数据表示的模型可能造成数据泄漏?)
后续
这一节主要讲的是 标准对偶SVM,旨在解决高维空间下,二次规划问题求解困难的问题,下面对比Linear SVM与Dual SVM:
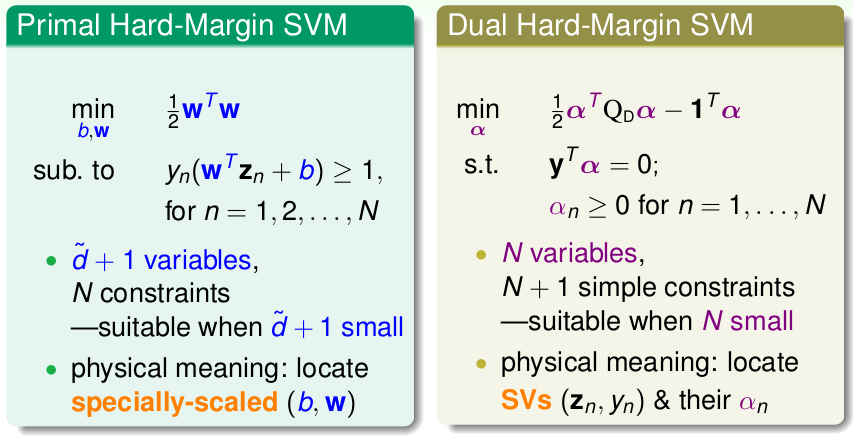
看起来我们的对偶问题的规模成功做到了只与数据样本量\(N\)有关,与高维空间的维度\(\tilde{d}\)无关,其实不然,实际内部的计算量还是很大的:
\(Q\)矩阵的元素: \(q_{n,m} = y_ny_m\mathbf{z}_m\mathbf{z}_n\),实际为\(R^{\tilde{d}}\)内的内积! 还是没有摆脱高维。不过对偶问题相比原始问题在非线性数据 的处理上,求解已经更加容易了。 至于如何在求解\(q_{n,m}\)的时候,彻底不再依赖\(\tilde{d}\),那就是下节的内容了,引入带核的SVM。