从这一节开始学习机器学习技法课程中的SVM, 这一节主要介绍标准形式的SVM: Linear SVM
引入SVM
首先回顾Percentron Learning Algrithm(感知器算法PLA)是如何分类的,如下图,找到一条线,将两类训练数据点分开即可:
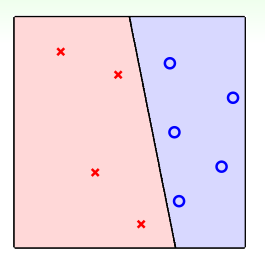
PLA的最后的直线可能有很多条,那到底哪条好呢?好坏的标准则是其泛化性能,即在测试数据集上的正确率,如下,下面三条直线都能正确的分开训练数据,那到底哪个好呢?SVM就是解决这个问题的。
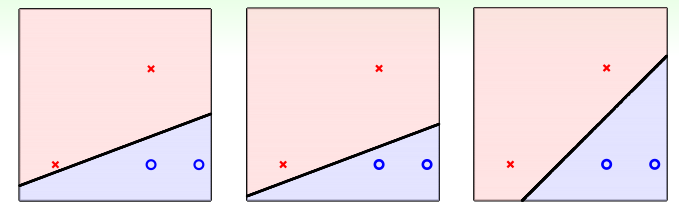
SVM求解
直觉告诉我们最右的要好一些,因为测试数据的分布应该与训练数据的分布类似,因此看起来它可以容忍更多的噪音,假设有一个数据在第一个红叉叉下方位置,也是属于叉类别,前两直线则容易把它分到圈圈的类别,而造成错误。因此理想的直线或者分类平面应该距离两类训练数据集越远越好:也就是下面的灰色区域越胖越好:
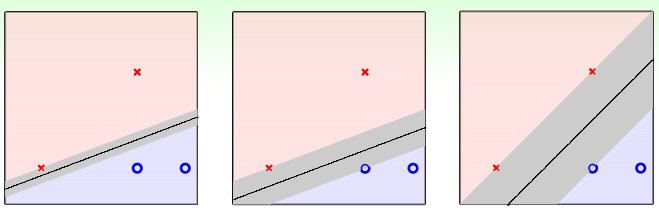
灰色区域的宽度是由直线与训练数据\(x_{1..N}\) 中到分类平面最近的距离决定的,这个距离称为margin,因此我们就可以将问题描述如下:
\[\begin{align} & \max\limits_{W,b}(margin(W,b)) \\ & s.t. y_n(W^TX_n+b) > 0 \end{align}\]
其中,分类平面由\(W,b\)决定,我们要找出最大\(margin\)的那条直线,这里的\(margin(W)=\min\limits_{n=1...N} distance(x_n,,W,b)\), 约束条件是这条直线已经将两类完全分开,即:\(y_n(X_n+b) >0\) 。下面我们看看点\((x_n)\)到平面\(W^TX+b = 0\)的距离,看下图:
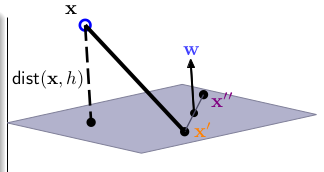
\(W\) 为平面\(W^TX+b=0\)的法向量,\(x^{'}\)与\(x^{''}\)为平面上的两个点,现在如果要求点\(X\)到平面的距离\(dist(X,W,b)\),即向量\(X-X^{'}\)投影(proj)到法向量\(W\):
\[distance(X,W,b)=\left | \frac{W^T}{\Arrowvert W\Arrowvert }(X-X^{'}) \right |= \frac{1}{\Arrowvert W\Arrowvert }|(W^TX +b) |\]
到此,再结合约束条件\(y_n(W^TX+b)>0, \ y_n \in \{-1, 1\}\), 点\(X\)到平面的距离可以通过去绝对值符号,转化为如下的式子:
\[distance(X,W,b)=\frac{1}{\Arrowvert W \Arrowvert }y_n(W^TX+b)\]
因此问题转化如下的优化问题:
\[\begin{align} & \max\limits_{W,b} \quad & margin(b,W) \\ & s.t. & every \ y_n(W^TX_n +b) > 0 \\ & & margin(b,W) = \min\limits_{n=1..N} \frac{1}{\Arrowvert W \Arrowvert}y_n(W^TX_n +b)\end{align}\]
另外,考虑到\(W^TX+b=0\)与\(2W^TX+2b=0\)这两个平面是同一个平面,只是对\(W,b\)经过了放缩(scaling),因此在缩放的过程中,不管是\(W,b\),还是\(2W,2b\), 都是对应同一个平面,因此求距离进行优化的过程不会有影响,利用这个特点,同时为了方便计算,对于某个的超平面,作出如下的假设放缩:
\[\min\limits_{n=1...N}y_n(W^TX_n+b) = 1\]
因为对于一个固定的平面,通过放缩,肯定存在一组\(W,b\)使得上述的等式成立,同时也保证了条件\(y_n(W^TX_n+b) >0\),这样\(margin(W,b) = \frac{1}{\Arrowvert W \Arrowvert}\),因此我们的优化问题转化为如下:
\[\begin{align} & \max\limits_{W,b} \quad \frac{1}{\Arrowvert W\Arrowvert} \\ & s.t. \quad \min\limits_{n=1...N}(y_n(W^TX_n+b)) =1 \end{align}\]
上述的约束条件是最小值等于1,对于优化问题来说,一般是某个等式或者不等式,这样容易求解,因此将上述的约束条件转为:\[y_n(W^TX_n +b) \geq 1, \quad for \ all \ n\]
考虑上述转换的正确性: 反证法,假设对于所有的\(n\), 有\(y_n(W^TX_n+b) > 1\), 即不满足最小值为1的条件,不妨设为\(\min = K, K>1\),设此时得到的最优解为\(W,b\),那么\(\frac{W}{K},\frac{b}{K}\) 很显然比\(W,b\)更优,矛盾。因此下面两式等价:
\[\begin{align}& \min(y_n(W^TX_n + b)) =1 \\ & y_n(W^TX_n+B) \geq 1, \ for \ all \ n \end{align}\]
再结合将求max转为min, 求距离,转为求平方等转化,最后我们的优化问题如下:
\[\begin{align} & \min\limits_{W,b} \quad \frac{1}{2}W^TW \\ & s.t. \ y_n(W^TX_n +b) \geq 1, \ for \ all \ n \end{align}\]
这个问题的优化方程为二次方程,条件为一次线性约束,是一个典型的二次规划问题(Quadratic Programming),而QP问题有很多解法,我们只需要将上述优化问题,转化为QP问题解法的格式,然后直接代入QP Solver,即可,如下:

左侧是我们最后的优化问题,右侧是标准的QP问题的输入格式,一共有4个输入变量: \(Q,p,A,c\), 及一个最终的优化结果: \(u\) ,我们只需要表示出上述四个输入变量,就可以输入到某个QP Solver里面即可,通过对应关系,表示如下:
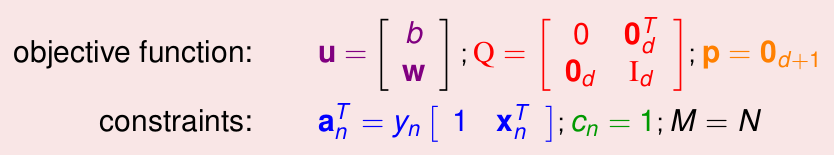
这样就可以得到最优的\(W,b\),进而求出\(g_{SVM} = sign(W^TX+b)\),进行后续预测。
上述的算法仅仅是最简单的线性SVM, 不过是其它类型SVM的基础,总结一下,流程很简单,如下:
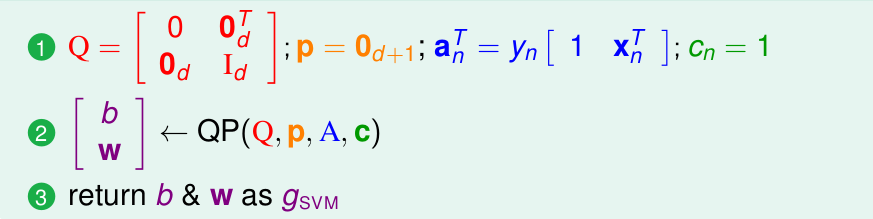
这种算法同样也可以解决非线性分类问题,通过之前的非线性转化,到线性空间: \(z_n = \phi(x_n)\),理论上即可直接应用到非线性问题中。不过缺陷也很明显,要求数据点必须线性可分,由于这个特点,这种算法也叫做: Linear Hard-Margin SVM。
SVM 与 VC 维
这里需要提一下,SVM(Support Vector Machine)的含义,我们了解到,SVM就是要找到最胖的那个分类面,如下:
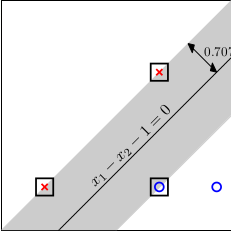
其中,在边界上的用黑框圈出来的三个点,我们就称为SV,Support Vector,因为它们才是求解过程中,真正起到作用的点,其余的点没有起到作用,后续的课程中也有进一步的介绍SV。
简单来说,SVM是基于PLA的一个算法,上面开始说了, 直觉告诉我们最胖的直线应该容错性好,其中的原理其实则是SVM相对于PLA,VC维降低了(注: 算法的VC维的定义不太明确,类比与\(\mathcal{H}\)的VC维定义即可, 这里只是定性的介绍),看下图:
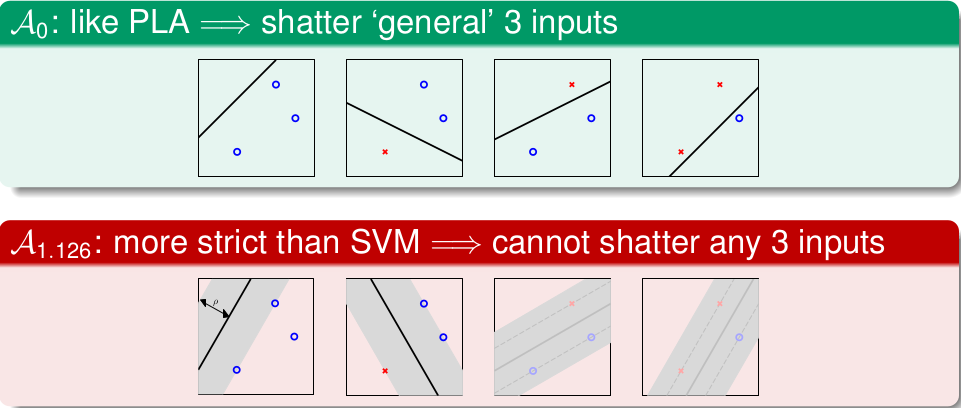
以三个输入的数据为例,PLA可以shatter(能够将\(2^3\)种情况都分开),而无法将4个数据点shatter,因此VC(PLA)=3,我们从另外一个角度来考虑, 假设我们规定了Margin的值为\(\rho\) ,也就是胖瘦的程度,那么肯定会存在输入数据量为3,且无法shatter的情形,比如上图的后两种,在\(\rho\)下 无法shatter,因此大致看起来,\(d_{VC}(\rho) < 3\)的。其实有严格的数学证明,可以得到:
\[d_{VC}(\rho) \leq d+1 = d_{VC}(PLA)\]
VC维减少了,意味着复杂度降低,也就是说更不容易overfitting,泛化性能更好,这也是就是我们要找最胖的分类面的原因。