接着练习TensorFlow, 这一节开始实现RNNs(循环神经网络), 同样使用mnist数据集,测试正确率也基本可以到99%。 同CNNs, RNNs的结构以及训练方式这里不加赘述,重心放在实现上。
提到循环神经网络(Recurrent Neural Networks),下面这张图就不得不说: 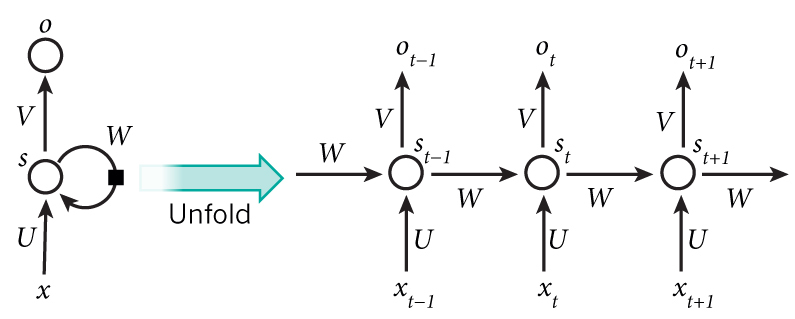
RNNs 主要处理时序数据,比如一句话,词与词之间都是有顺序的,因此经常用在NLP领域,比如机器翻译,情感分析等。 一般的RNNs有多个FNN横向连接而成,其中中间有个rnn-cell, 存储的是前面序列的隐含状态s。 分解开来的话, 就相当于三层,第一层是输入x到rnn-cell的连接,第二层是rnn-cell,得到的是隐藏状态s,第三层是rnn-cell到输出o的连接层。下面开始一步一步实现。
第一步我们需要想办法把mnist的数据定义为时序数据,开始数据是 28X28的,因此我们可以按行来看,第一行是第一个时间点,下一行是第二个时间点的 数据,对应到上图就是: 第一行的数据是\(x_0\),第二行的数据为\(x_1\),依次类推。 另外,这一节我们主要用RNNs做分类,因此只关心最后一个时间点的输出即可。因此我们实现的结构其实是下图这样的: 下一节会讨论回归问题,就是考虑所有输出:
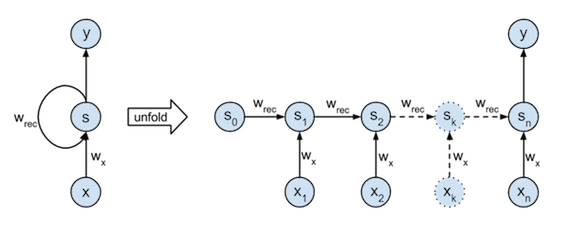
首先定义一些后面使用的参数:
1 |
|
接着定义TensorFlow的输入:
1 | # tf input |
RNNs每一个单元里面包含一个三层的普通神经网络, 因此我们事先设置一下这里面的权重矩阵和偏置,需要注意的是,RNNs的一个特点就是权值共享,所有层用的权重矩阵一样 :
1 | # W & b |
下面开始定义RNNs网络结构 首先输入层到rnn-cell:就是一个简单的前馈层,不过要特别注意数据的维度
1 | # hidden_layer for input |
接着是中间的cell,这个TensorFlow作了很好的封装,我们只需要传入需要的参数就可以了: 1
2
3
4# RNN cell
with tf.name_scope("RNN_CELL"):
lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_unins) #根据隐层的神经元个数,定义一个基本的Cell
outputs, states = tf.nn.dynamic_rnn(lstm_cell, X_in, dtype=tf.float32) # 传入lstm_cell与上层的输出:X_in即可
这里有点需要说明的是,本来RNN是需要一个初始状态的,这样才能够向后传递,但是TensorFlow可以随机产生一个初始状态矩阵,但是需要在tf.nn.dynamic_rnn的参数里面指定dtype=tf.float32,不然会报错。当然可以向下面的指定初始状态:
1 | lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_unins) #根据隐层的神经元个数,定义一个基本的Cell |
这里的输出states表示最后隐层的状态tuple, 实际value在states[1]内。 前面已经说了,我们只需要最后的输出结果,因此只需要加一个输出层就好:
1 | # out layer |
到此,网络结构构建完成,后续便是cross-cost, accuracy,这与前面基本一样:
1 | pred = RNN(xs, weights, b) # 这里将上述的层,定义为了一个函数 |
运行结果如下,正确率可以接近99%,但是比CNN训练快一倍时间, 通过调整参数,应该可以到99%+,从此可以看出来,虽然我们是强行将图片变为时序数据,但是效果也很好,看来RNN的适用范围还是蛮广的.
1 | epoch: 1 accuracy: 0.9519 |
完整代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88#!/usr/bin/env python
# encoding: utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
# hyperparameters
lr = 0.001 # learning rate
batch_size = 128
n_inputs = 28 # 28 cl
n_steps = 28 # 28 rows -> time stamps
n_hidden_unins = 128 # hidden units
n_classes = 10
# tf input
xs =tf.placeholder(tf.float32, [None, n_steps, n_inputs], name="inputs")
ys =tf.placeholder(tf.float32, [None, n_classes], name="outputs")
# W & b
weights = {
'in': tf.Variable(tf.random_uniform([n_inputs, n_hidden_unins], -1.0, 1.0), name="in_w"),
'out': tf.Variable(tf.random_uniform([n_hidden_unins, n_classes], -1.0, 1.0), name="out_w"),
}
b = {
'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_unins]), name="in_bias"),
'out': tf.Variable(tf.constant(0.1, shape=[n_classes]), name="out_bias"),
}
def RNN(X, weights, bias):
# hidden_layer for input
# X : (128, 28, 28)
with tf.name_scope("inlayer"):
X = tf.reshape(X, [-1, n_inputs])
X_in = tf.matmul(X, weights['in']) + b['in']
X_in = tf.reshape(X_in, [-1, n_steps, n_hidden_unins])
# RNN cell
with tf.name_scope("RNN_CELL"):
lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(n_hidden_unins)
# _init_state = lstm_cell.zero_state(batch_size, dtype=tf.float32)
# ouputs, states = tf.nn.dynamic_rnn(lstm_cell, X_in, initial_state=_init_state)
outputs, states = tf.nn.dynamic_rnn(lstm_cell, X_in, dtype=tf.float32)
# out layer
with tf.name_scope('outlayer'):
results = tf.matmul(states[1], weights['out']) + b['out']
return results
pred = RNN(xs, weights, b)
# cost
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, ys))
train_op = tf.train.AdamOptimizer(lr).minimize(cost)
# accuracy
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(ys, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# run
import time
init = tf.global_variables_initializer()
epochs = 15
st = time.time()
with tf.Session() as sess:
writer = tf.summary.FileWriter('logs/', sess.graph)
sess.run(init)
batch = mnist.train.num_examples / batch_size
for epoch in range(epochs):
for i in range(int(batch)):
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape([batch_size, n_inputs, n_steps])
sess.run(train_op, feed_dict={xs: batch_x, ys: batch_y})
print 'epoch:', epoch+1, 'accuracy:', sess.run(accuracy, feed_dict={xs: mnist.test.images.reshape([-1, n_steps, n_inputs]), ys: mnist.test.labels})
end = time.time()
print '*' * 30
print 'training finish.\ncost time:',int(end-st), 'seconds\naccuracy:', sess.run(accuracy, feed_dict={xs: mnist.test.images.reshape([-1, n_steps, n_inputs]), ys: mnist.test.labels})