前段时间看完了机器学习基石课程,不过还有regularzation和 validation 没有整理,由于需要,先看了技法课程中的神经网络(Neural Network)。林老师讲的依然很好,将神经网络笔记记录于此。
神经网络的提出
首先之前讲过了PLA(Percetron), 对于一个线性可分的数据,我们可以用一条直线来分开; 下面看一个多个percetrons的模型,直接看下面的图: 稍微复杂点的2层的percetron:
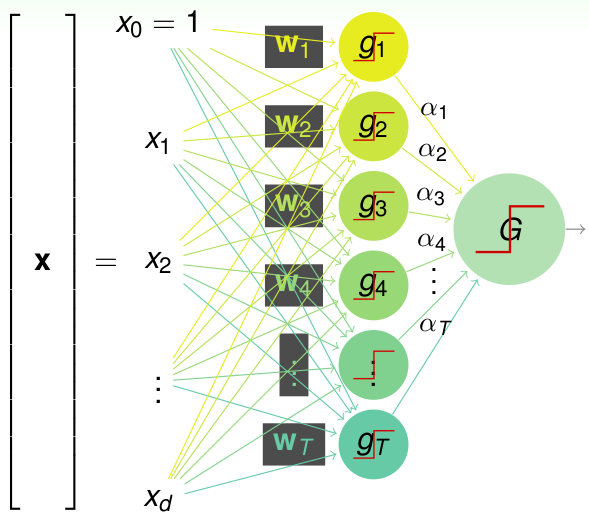
首先给了输入\(\textbf{x}\),是\(d\)维的vector, 然后首先经过一堆的sign函数,得到了T个g函数,然后再次通过一层\(\alpha\)参数选出最终的结果G,用以下的假设空间函数表示:\[G(\textbf{x})=sign(\sum\limits_{t=1}^{T} \alpha_t sign(\textbf{w}_t^T\textbf{x}))\]这个2层的percetron其实就可以表示一些简单的逻辑操作了,比如下面的两个g的例子:

我们如果要表示最右边的区域,即\(AND(g_1, g_2)\),我们可以这样赋值:\(\alpha_0 = -1, \alpha_1=1, \alpha_2=1\),这样方程式变为:\[G(\textbf{x})=sign(g_1(\textbf{x}) + g_2(\textbf{x}) - 1)\]也就是说只有当\(g_1 = g_2 = 1\)时,\(G=1\),其余情况都为0。这样就可以分类了。同样我们可以用\[G(\textbf{x})=sign(0.5 g_1(\textbf{x}) + 0.5 g_2(\textbf{x}) +1 )\]来表示\(OR(g_1, g_2)\)等等。我们可以发现这种两层的percetron十分的powerful,只要我们有足够多的Percetron,就可以划分更细致区域,比如说有足够多的直线,然后执行AND操作,就可以围出来一个近似圆的情况:
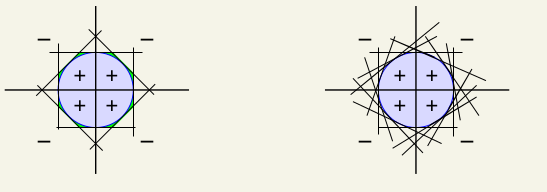
但是这样还是有很多不足的,首先是percetron越多,那么模型的复杂度或者说\(d_{vc}\)就会变大。再者上述的两层模型是无法表示出\(XOR\)(异或)操作的,也就是说,我们经过两次转化,是无法实现\(XOR\)的操作的,但是如果我们再加一层呢? 是不是就可以解决了,如下:
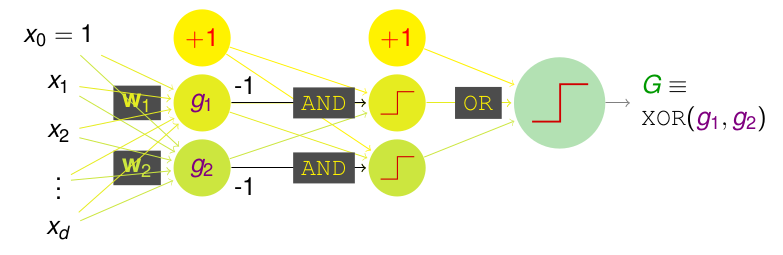
转换为方程式,即:\(XOR(g_1,g_2)=OR(AND(-g1, g_2), AND(g_1,-g_2))\),我们会发现,只有\(g_1 \neq g_2\)时,该式才为1,因而达到了XOR。
从最简单的一层Percetron只可以分类线性可分的数据,到二层的可以分出凸多边形的数据,再到三层的可以分XOR这种无法线性可分的数据,我们发现,层数越多,能力就越强。这里也就引出了神经网络,即:多层感知机(Multi-Layer Percetrons),为什么叫做神经网络呢?想想人类的神经元组织,是不是也就是一个一个神经元互相连接,跟我们的感知机很类似,神经元就是上述的一个个的\(g\),神经元的连接就对应这感知机中的权重,最后神经元需要对其它神经元传过来的信号作处理,这个过程就对应上述的sign函数,即转换函数(也叫激活函数)。因此上述一层层的感知机就组成神经网络。
Hypothesis 假设空间
前面引出了神经网络,这一节主要深入探究层与层之间的联系方式。首先再看一下我们的神经网络模型:
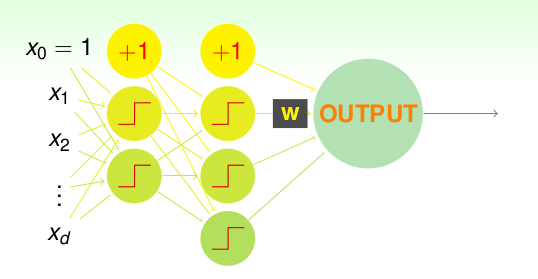
先考虑最后的输出层,这个比较容易,因为我们一般解决分类或者回归问题的,所以说一般我们就用一个前面介绍过的linear model 即可,如下
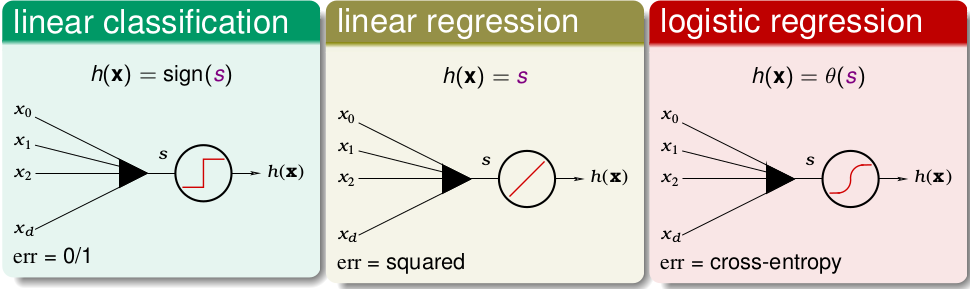
在文中会以linear regression作为例子讲解,这就意味着使用square error作为cost funtion。如果我们想分类的话,最后一层的激活函数就可以使用logistic regression记性二分类,或者 softmax 进行多分类,这时候就用 cross-entropy作为cost funtion了,别的地方都不会变化。
现在开始考虑中间层的神经元的(也叫隐含层Hidden Layer)的激活函数,分别考察上述三种函数:
如果层与层之间激活函数都用线性函数表示,其实没有意义了,想想我们这么多层都使用线性连接,其实最终整理出来,输出层还是关于输入层的线性关系,没有意义!
使用sign函数的话,输出0或者1,正对应到了神经元的激活与否,然而依然存在老问题,由于是离散值函数,很难去优化。
使用第三种的非线性但是平滑的函数作为激活函数(转化函数)是最常见的选择。因为是很接近sign的一个平滑函数,因而很容易优化。常用的有\(\sigma(s) = sigmoid(s)= \frac{1}{1+e^{-s}}\),\(tanh(s)=\frac{e^{s} - e^{-s}}{e^s + e^{-s}}=2\sigma(2s)-1\)等,还有其它选择如 Relu等,在某些场景下效果很好。
接下来会以\(tanh\)作为我们的激活函数。
至此,我们已经将所有层之间的激活函数确定好了,因此神经网络的Hypothesis就很明确了,输入层将数据传给后续的隐含层,一直得到最后的输出即可,为了方便描述,我们定义好各个参数,变量的名字,如下图:

假设我们一共有包含输入层和输出层\(L+1\)层的网络,且第\(i\)层的神经元(节点)个数为\(d^{(i)}\),这样就构成了\(d^{(0)}-d^{(1)}- ... - d^{(L)}\) Neural Network。 下面解释上述参数的意义:\[w_{ij}^{(l)}: \begin{cases} 1 \leq l \leq L & layers \\ 0 \leq i \leq d^{(l-1)} & inputs \\ 1 \leq j \leq d^{(l)} &outputs \end{cases}\] \(w_{ij}^{(l)}\)指的是第\(l-1\)层的第\(i\)个神经元与第\(l\)层的第\(j\)个神经元之间的权重值。\[\ s_j^{l} = \sum\limits_{i=0}^{d^{(l-1)}}x_i w_{ij}^{(l)}\] \(s_{j}^{(l)}\)指的是第\(l\)层的第\(j\)个神经元的score(得分),也可以当作该神经元的输入。\[x_{j}^{(l)} =\begin{cases} tanh(s_{j}^{(l)}) & \text{ l = L} \\ s_{j}^{(l)} &l=L \end{cases}\] \(x_{j}^{(l)}\)是第\(l\)层第\(j\)个神经元的经过激活函数对其输入\(s_{j}^{(l)}\)的输出,特别的是最后的输出层,因为我们以Linear Regression为例子,直接将 \(s_1^{L}\)作为最后的输出: \(x_{1}^{(L)}\)(最后一层仅仅有一个神经元)。
这样我们只需要将输入数据赋给\(\textbf{x}^{0}\),然后一层一层计算\(\textbf{x}^{l}\),最后得到我们的预测值: \(\textbf{x}_{1}^{(L)}\)。到此Hypothesis已经明确了,下面就是如何使用训练数据学到所有的参数。一般都说NN的训练时间很长,我们先看看有多少参数需要计算:\[count(W) = \sum\limits_{i=0}^{L-1} (1+d^{(i)})d^{(i+1)}\] 每一层需要加一个常数,上图中的最上面那个(就是偏置项bias)。所以说参数经常上万,因此训练时间很长。这个问题后续还会讲到,下面就是开始如何从数据中学到那一堆的参数,也就是training的过程。
模型的训练
训练的目标很简单,跟之前的模型一样,就是要求出最小化cost function的值\(E_{in}\)的各个参数\(w_{ij}^{(l)}\),上面我们也提到了使用平方误差表示cost function,即: \(e_{n} = (y_n - NNet(\textbf{x}_n))^2\),其中NNet是神经网络预测的值,\(y_n\)是数据的真实值。有了cost function,那我们就可以尝试使用梯度下降(Gradient Descent)来求最优解,即: \[ w_{ij}^{(l)} \gets w_{ij}^{(l)}- \eta \ \frac{\partial e_n}{\partial w_{ij}^{(l)}}\]这里我们使用随机梯度下降(SGD)来计算梯度,也就是每次只选择一个数据点。接下来就是求梯度了\(\triangledown e_{n}\),这里会介绍误差反向传播的算法(Back Propagation)
再看神经网络的图模型:

我们先尝试看看最后一层的参数: \(w_{i1}^{(L)}\),先看看\(e_{n}\)与\(w_{i1}^{(L)}\)的关系: \[e_{n}=(y_n - s_{1}^{(L)})^2 =(y_n - \sum\limits_{i=0}^{d^{(L-1)}}w_{i1}^{L}x_{i}^{(L-1)})^2 \]我们可以看到\(e_{n}\)是先影响了\(s_{1}^{L}\),然后\(s_{1}^{(L)}\)再影响\(w_{i1}^{(L)}\)。所以我们可以用求微分的链式法则,来间接求梯度,如下:
\[\begin{align*}\frac{\partial e_{n}}{\partial w_{i1}^{(L)}} &= \frac{\partial e_{n}}{\partial s_{1}^{(L)}} \cdot \frac{\partial s_1^{(L)}}{w_{i1}^{(L)}} \\ &= -2(y_n - s_1^{(L)}) (x_i^{(L-1)}) \end{align*}\]这个式子的变量都是已知的,我们可以很轻松的求出最后一层的参数: \(w_{i1}^{(L)}\)。那么隐含层(Hidden Layer)的呢?同理,我们也可以写出类似上述的等式:\[\begin{align*}\frac{\partial e_{n}}{\partial w_{ij}^{(l)}} &= \frac{\partial e_{n}}{\partial s_{j}^{(l)}} \cdot \frac{\partial s_j^{(l)}}{w_{ij}^{(l)}} \\ &= \delta_j{(l)}(x_i^{(l-1)}) \end{align*}\]这是对\(w_{ij}^{(l)}\)的求微分,其中\(1 \leq l < L,\ 0 \leq i \leq d^{(l-1)},\ 0 \leq j \leq d^{(l)}\),这里我们新引入了一个变量\(\delta\): \(\delta_{j}^{(l)} = \frac{\partial e_n}{s_j^{l}}\),来表示cost function 对第\(l\)层的第\(j\)个神经元的输入的微分,只需要求出了\(\delta\)那么\(\frac{\partial e_{n}}{\partial w_{ij}^{(l)}}\) 也就知道了,下面开始求,这也是反向传播的核心所在。
首先看看\(e_n\)是如何一层层的影响着\(s_j^{(l)}\)的,如下:
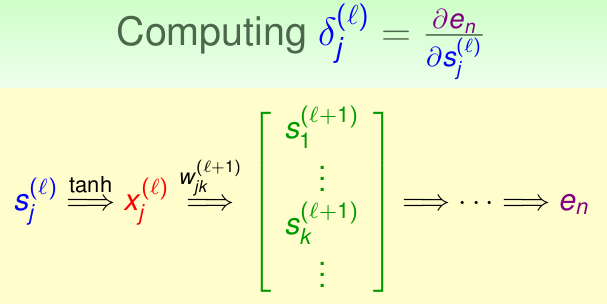
只考察最近三层的影响如下,我们同样应用链式法则,首先考虑上图绿色的\(s_k^{l+1}\),继而是前一层的\(x_j^{(l)}\),最后通过激活函数作用到\(s_j^{(l)}\):
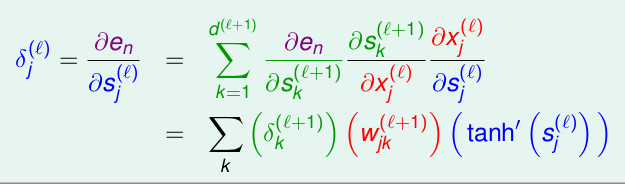
这样我们就可以得到了一个递推关系: \(\delta_{j}^{(l)}\)是由\(\delta_{k}^{(l+1)}\)表示的,也就是要计算\(l\)层的参数,需要使用\(l+1\)的\(\delta\),这就是为什么叫Back Propagation反向传播的原因,训练过程需要从后往前计算。因为我们已经求出了最后一层的参数: \(\delta_1^{(L)} = -2(y_n - s_1^{(L)})\),这里面的都是已知的,其中\(s_1^{(L)}\)就是我们的预测值,是因为最后一层的激活函数是采用了Linear Regression的线性函数,$ = s_1^{(L)}\(,那么我们就可以计算出\)L-1\(的\)$: \[\begin{align*}\delta_{i}^{(L-1)} &= \frac{\partial e_n}{\partial s_j^{(L-1)}} \\ &= \frac{\partial e_n}{s_1^{(L)}} \cdot \frac{s_1^{(L)}}{x_j^{L-1}} \cdot \frac{\partial x_i^{(L-1)}}{\partial s_j^{(L-1)}} \\ &= \delta_1^{L} \cdot w_{i1}^{L} \cdot tanh^{'}(s_j^{(L-1)})\end{align*} \]这样我们就把所有的倒数第二层\(L-1\)的\(\delta\)求出来了,然后再依次向后求出所有的\(\delta\),从而可以使用SGD得到所有的\(w_{ij}^{(l)}\),这样一轮训练完成。
现在就可以给出整个训练算法(BackPropagation)的流程了:

需要注意的是,算法主要分为两部分,开始需要初始化所有参数\(w_{ij}\),一般情况是随机化,而非0, 然后就是随机梯度下降的过程,选择一个点,利用当前的参数,从前向后依次计算所有的\(x_i^{(l)}\),之后反向计算所有的\(\delta_{j}^{(l)}\), 最后更新\(w_{ij}^{(l)}\),经过多次迭代或者达到设定误差函数的一个阈值之后,模型就训练完毕,返回 \(g_{NNET}\)。 这里有一点优化是,除了使用SGD之外,我们一次不再训练一个数据,也不训练所有的数据,而是可以一次性训练一批数据,这样是一种折中的方式,叫做Mini-batch Gradient Densent(MBGD),这样会加快训练速度,在后续实现中,会使用。
神经网络的优化
VC维
首先看看神经网络的复杂度,这里给出神经网络的VC-Dimension: \(d_{vc} = O(VD)\),其中\(V\)是神经元的个数,\(D\)是权重或者说参数的个数,这个是根据参数的个数得到模型的自由度近似得到的。我们可以发现,如果神经元的数量很多,那么可以解决几乎所有的问题,但是同样神经元越多,那么VC维也就越大,就越容易产生 overfitting,泛化误差可能会很大。
正则化
我们知道,神经网络的参数很多,为了防止过拟合,就需要加上正则项进行约束,尽可能的减少参数的个数,但是应该加入什么正则项呢?首先考虑常用的二范式:\[\Omega(\textbf{w})=\sum(w_{ij}^{(l)})^2\]然而这里并不是最好的。因为它并不能减少参数的个数,因为这个正则项属于一个等比缩放,大的权重就缩小比较厉害,小的权重缩小的比较轻,比如一个参数是10,缩放之后是8,那么假设有个参数是5,那么放缩之后就得到了4。这样大的变小了,小的同样也变小了,但是都不会变成0。这样我们的复杂度其实并没有降低。当然那\(\sum\|w_{ij}^{(l)} \|\)虽然可以减少复杂度,然而并不能微分,这样就不能优化了。我们需要的是,他们变化的幅度应该差不多,就是说,大的参数缩小缩小一个中等范围,小的参数也缩小中等效果,这样小的参数就会慢慢变成0。在 实际中,经常使用如下的 regualizer: \[\sum\frac{(w_{ij}^{(l)})^2}{1+(w_{ij}^{(l)})^2}\]
Early Stopping
除了正则化,还有一个常用的方式就是EarlyStopping,就是再达到\(E_{in}\)最小之前就停止迭代,争取找到最优的参数,至于具体迭代多少次,这个就是需要用Validation里面的方法了,使用交叉验证等方式来找到\(E_{test}\)最小的迭代次数。
总结
这一章主要介绍了最基本的神经网络(Neural Network),层数越多,能做的事情就越多,数据通过一层层的神经元以及激活函数,萃取有用的特征。后续又介绍了BackPropagation算法去训练。由于神经网络的参数众多,因此要使用一些trick来加快训练和避免过拟合,主要是正则化以及提前停止。看完之后,对神经网络有了基本的认识,后续还需要自己实践一遍才能加深理解!