引入
前面介绍了PLA,Linear Regression 和 Logistic Regression 这三种线性分类(回归)模型,已经知道可以很好地用来处理线性可分的数据集或者说大概可以线性可分,然而现实世界中很多数据并不是线性可分的,起码很难找到一个超平面去分开两类数据,而Linean Model的限制也就是无法很好地处理无法用超平面区分的数据,这种数据很常见,如下图的一个2维数据集: 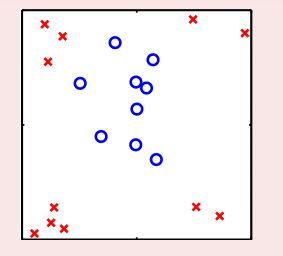
不过,我们可以发现,虽然它不是线性可分,但是貌似可以曲线可分,比如下面的分类方式: 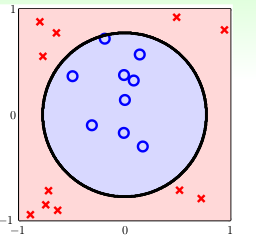
我们可以把圆内的数据划分为o,圆外的数据归为x,看起来很不错,再进一步抽象出如下的模型,\(h_{SEP}=sign(r^2-x_1^2-x^2_2)\) 用来解决上述的问题:其中\(r\)为上述的圆的半径,这并不是线性的,而是高阶多项式的,在优化求解的时候,会相对麻烦,这就引出了这节的非线性转换,将非线性的hypothese转为线性,这样我们才可以用我们之前学得线性知识去求解。
非线性转换
上述我们得到了\(h_{SEP}=sign(r^2-x_1^2-x^2_2)\),我们做如下的转换: \[\begin{aligned} \color{orange}{h}(x) &= (\; \underbrace{\color{orange}{r^2}}_{\color{orange}{\tilde{w}_0}}\cdot\underbrace{\color{purple}{1}}_{\color{purple}{z_0}} + \underbrace{(\color{orange}{-1})}_{\color{orange}{\tilde{w}_1}}\cdot\underbrace{\color{purple}{x_1^2}}_{\color{purple}{z_1}}+ \underbrace{(\color{orange}{-1})}_{\color{orange}{\tilde{w}_2}}\cdot\underbrace{\color{purple}{x_2^2}}_{\color{purple}{z_2}} \;) \\ &= sign(\color{orange}{\tilde{w_0}}+\color{orange}{\tilde{w_1}}\color{purple}{z_1}+\color{orange}{\tilde{w_2}}\color{purple}{z_2}) \\ &=sign(\color{orange}{\tilde{w}^T}\color{purple}{z}) \end{aligned}\] 这样就变成线性的Hypothese。这里面其实将 X-Space转换到了Z-Space,或者说换了坐标系(基),X下的一个圆就对应了Z下的一条直线。如下图,左边是X-Space的数据点,右边是一一对应的Z-Space的数据点:

作了上述转换之后,我们只需要对\(\mathcal{D}^{'}_{z} = \{ (z_n, y_n)\}\),其中\(z = \phi(x)=(1, x_1^2, x_2^2)\)作为样本数据,然后使用之前学过的线性分类模型来求就可以了。
上述的2D分类问题,我们使用一个标准圆作为区分面,但是有时候可能是一个圆心不在原点的圆,再或者是一个椭圆,双曲线等等,这时候,我们可以使用一般的二次曲面即: \(\textbf{z} = \phi_2(\textbf{x})=(1, x_1, x_2, x_1^2, x_2^2, x_1x_2)\),然后\(\textbf{w}=(w_0, w_1, w_2, w_3,w_4, w_5)\)。这样我们就将X-Space的非线性数据点,转换为Z-Space的线性数据点来分类,转换函数为\(\phi(\textbf{x})\),总结主要步骤如下:
- 将原始X数据\(\{(\textbf{x}_n, y_n)\}\) 转换为Z数据:\(\{(\textbf{z}_n=\phi(\textbf{x}_n), y_n)\}\)
- 使用线性分类方法: PLA/Pocket,Linear Regression, Logistic Regression等求解 \(\textbf{w}\)
- 返回假设函数: \(g(\textbf{x}) = sign(\textbf{w}^T \phi(\textbf{x}))\) 用来分类新的点。
转换模型复杂度
额外的代价
看起来问题解决的很好了,所有的分类问题都可以做了,因为我们不止可以做二次阶转换,还可以做三阶转换等等, 只要数据集可分,那么我们一定可以通过转换函数\(\phi(x)\)来转换到我们已经知道的线性分类上! 但是真的有这么好的事情吗? 现在我们只知道通过非线性转为线性,是一定可以解决分类的,但是我们有没有付出额外的代价呢?
一个最直接的代价就是存储空间变大了,比如开头的2D例子里面,本来只有\((1, x_1, x_2)\)三维数据,结果映射之后,变成了\(1, x_1,x_2, x_1^2, x_1x_2, x_1^2,x_2^2\),变成了6维!求解的参数也就是6维,因此需要一倍的空间去存储。
其次在考虑模型复杂度,假设原始数据 \(\textbf{x} \in R^d\),经过\(Q\) 阶的转换(上述例子中Q=2),首先看看我们的\(\phi_{Q}(\textbf{x})\)为:
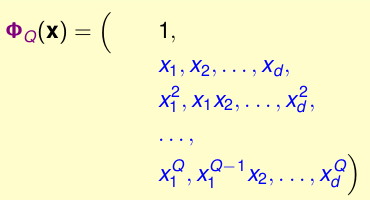
一共有\(1+\widetilde{d}\)种,其中1是\(x_0\),剩下的\(\widetilde{d}\)是剩下的数量。总的数量其实就相当与从\(Q+d\)中找Q个元素,即:\(C_{d}^{(Q+d)} = O(Q^d)\),因此模型的自由度也就是\(O(Q^d)\),前面介绍VC维的时候,我们知道模型自由度,可以近似为VC维:\(1+\widetilde{d} = d_{vc}(\mathcal{H}_{\phi_Q})\),因此阶数Q越大,VC维就越大,模型复杂度就越大,而且这个增长是指数级的,这样并不好,因为根据:

\(d_{vc}\)越大,虽然\(E_{in}\)会变小,不过\(E_{out}\)会变大,也就是说容易发生后面讲的过拟合。
如何选择参数-不能偷看数据
既然这样,那我们应该如何选择阶数Q呢?用眼看吗? 比如前面的2维例子,我们看原始数据,感觉用个二维曲线可以很好的分类,于是首先选择如下的二阶转换:\[\phi_2(x)=1,x_1,x_2,x_1^2,x_1x_2,x_2^2),d_{vc}=6\]后来你又觉得我用个圆就好了呀,于是又改为如下的转换:\[\phi_2(x)=(1,x_1^2,x_2^2),d_{vc}=3\]这样模型复杂度降低了。然后呢你多多观察了数据,又发现我就直接使用一个标准圆就好了: \[z=(1,x_1^2+x_2^2)\;,d_{vc}=2\]不错,你又降低了复杂度,只需要两个参数就好了,然后开心的算出来一个\(E_{in}\)很低的参数,结果计算发现\(E_{out}\)很糟糕,问题出在了哪里了?我的复杂度这么低,怎么会发生过拟合呢?泛化错误这么高?问题就出在你不该去偷看你已有的数据!原因有二:
你根据自己看原始数据的结论,去选择模型,这时候你的大脑已经替计算机承担了相当部分的复杂度,因此模型复杂度并不是你看到的\(d_{vc}=2\)
你偷看了现在这份数据,然后选择了标准圆,\(E_{in}\)很小,但是如果再来一个新的数据集\(\mathcal{D}\)呢?你看了之后,可能就不会用标准圆去刻画了!
因此,为了不发生过拟合,不要去事先偷看数据,或者说不要太信赖自己已有的那很少的数据。再者说了,现在是二维数据,可以画个图来参考参考,那10维呢? 也就很难去想象了。
假设空间的变化
再看不同阶的转换函数:
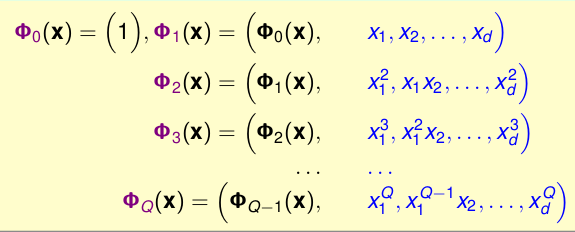
我们可以发现,其实有递推的关系,\(\pgi_{Q}(\textbf{x})\)包含着,\(\pgi_{Q-1}(\textbf{x})\)阶的所有项与Q阶部分组成的。也就是说,阶数大的可以表示的空间肯定包含阶数小的空间,即他们的\(\mathcal{H}\)有如下的关系:
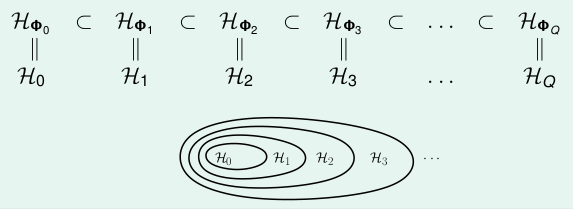
我们也知道了Q越大, \(d_{vc}\)就越大, 因此又有如下的关系:
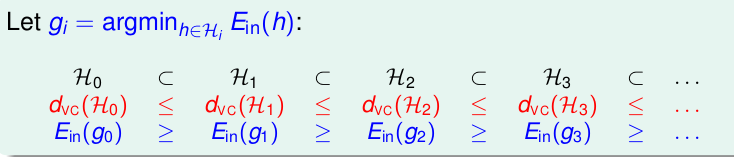
这个跟我们前面提到的很吻合。阶数越高越容易发生过拟合,泛化误差越高,因此原则是Linear Model First,如果我们可以用线性模型就可以得到\(E_{in}\)很低的结果,那就不要考虑高维的非线性转化了,代价很大!