11.25日更新: Linear-Regression练习
前面的学习基本都是介绍机器学习可以学习的原因。这里开始讲如何学习。也就是如何选择算法去找到最好的hypothesis.接下来几篇将会介绍线性模型，包括前面的PLA(感知机), 以及这一节的Linear Regression(线性回归)，还有下一节的Logistic Regression(逻辑回归)，以及它们的联系。
模型
仍然拿申请信用卡为例，PLA算法是用来判断给不给信用卡的，而如果我们想要知道给多少额度呢？ 这个时候，我们可以就可以直接使用\(score=W^TX\)值了，而不用sign函数了。因此就可以很容易的定义出Linear Regression的模型:\[ y= \sum\limits_{i=0}^{d}w_ix_i=W^TX\]是不是跟PLA:\(y=sign( \sum\limits_{i=0}^{d}w_ix_i)\)很像。注意，这里面的\(W,X\)都是\((d+1)\)维的列向量。下面就是开始找到一个算法来找到最好的h即可。
我们的数据集是\(D=\{ (x_1, y_1),...,(x_n,y_n)\}\)，那么最好的\(h(x_i)\)得到的\(\hat{y_i}\)应该与\(y_i\)很接近，这样自然而然就可以想到使用如下的损失函数作为评估每个h的标准:\(err(\hat{y},y) = (\hat{y}-y)^2\)那么训练数据集\(D\)对应的损失就应该是\[err(w) = E_{in}(w) = \frac{1}{N}\sum\limits_{i=0}^{N}(\hat{y}_i-y_i)^2=\frac{1}{N}\sum\limits_{i=0}^{N}(w^Tx_i-y_i)^2\]
下面的事情就是如何求出使得这个\(err\)最小的\(w\)。先化简为矩阵的形式:\[\begin{aligned} E_{in}(\color{blue}{w}) &= \frac{1}{N}\sum_{n=1}^{N}(\color{blue}{w^T}\color{red}{x_n}-\color{purple}{y_n})^2=\frac{1}{N}\sum_{n=1}^{N}(\color{red}{x_n^T}\color{blue}{w}-\color{purple}{y_n})^2 \\\ &=\frac{1}{N}\begin{Vmatrix} \color{red}{x_1^T}\color{blue}{w}-\color{purple}{y_1}\\\ \color{red}{x_2^T}\color{blue}{w}-\color{purple}{y_2}\\\ ...\\\ \color{red}{x_N^T}\color{blue}{w}-\color{purple}{y_N} \end{Vmatrix}^2 \\\ &=\frac{1}{N}\begin{Vmatrix} \color{red}{\begin{bmatrix} --x_1^T--\\\ --x_2^T--\\\ ...\\\ --x_N^T-- \end{bmatrix}} \color{blue}{w} - \color{purple}{\begin{bmatrix} y_1\\\ y_2\\\ ...\\\ y_3 \end{bmatrix}} \end{Vmatrix}^2 \\\ &=\frac{1}{N}|| \underbrace{\color{red}{X}}_{N\times (d+1)}\;\;\; \underbrace{\color{blue}{w}}_{(d+1)\times 1} \; - \; \underbrace{\color{purple}{y}}_{N\times 1} ||^2 \end{aligned}\]
这样我们的目标就是:\(\min E_{in}(w) = \frac{1}{N}\begin{Vmatrix}{X}{w}-{y}\end{Vmatrix}^2\), 这个可以近似看成关于\(w\)的二次函数，图像大致如下: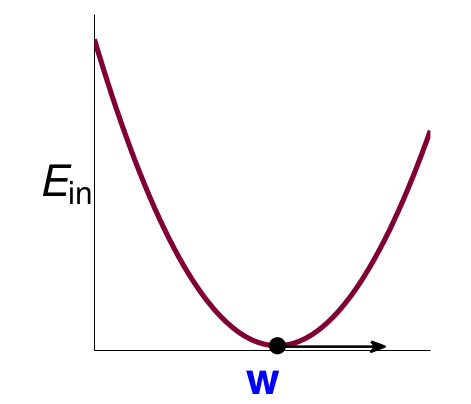
这个是凸函数，因此我们可以通过求一阶导数然后为0的\(w\)即可。这就是线性代数的范围了，类比二次函数即可，结果如下:
\[\nabla E_{in}(w)=\frac{2}{N}(X^TXw-w^TX^T)\] 接下来的事情就简单了，让\(\nabla E_{in} = 0\), 可以得到我们的最优的参数\(w_{lin}\):
\[w_{lin} = (X^TX)^{-1}X^Ty\]，我们一般把\((X^TX)^{-1}X^T\)设为 pseudo-iinverse: \(X^{\dagger}\), 这样我们经常这样写:\(w_{lin}=X^{\dagger}y\)。另外需要注意的，这是在\(X^TX\)可逆的情况下，也就是\(X\)满秩，如果不可逆的情况下，会使用其它方式定义，比如岭回归，就是对\(X^TX\)进行修正，这里不多说。到此为止，我们求出了最优的\(w\), 这样再来一个新的数据点\(X\), 那么预测值就是:\[\hat{y} = X w_{lin} = XX^{\dagger}y\]
现在，我们可以给出完整的线性回归算法了: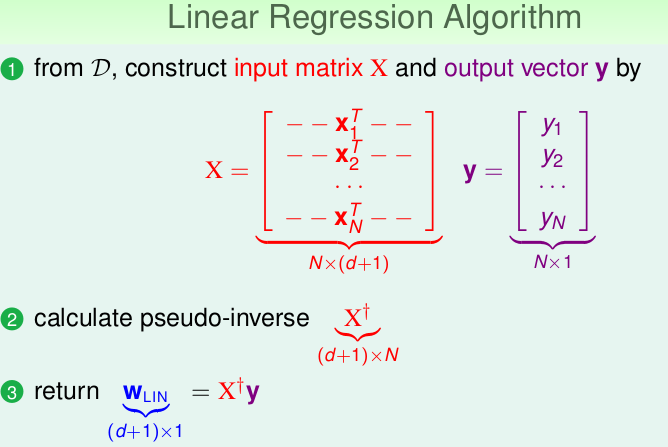 
小结
我们可以看到，线性回归模型并不是一次一次的迭代获得最优解的过程，而是一次求解就可以，这个就归功于损失函数有解析解。复杂度都集中在求逆的过程，效率还是很高的。