Alias Method离散分布随机取样

文章目录

1. Alias-Method 原理
2. 代码

在图的随机游走中，有一块需要随机取样， 比如当前到达v节点，那么下一次随机会到达哪个节点。这种问题其实就是离散分布的随机变量的取样问题。 查了一些资料， 发现Alias Method 是一种很高效的方式。在初始好之后，每次取样的复杂度为\(O(1)\)。 下面介绍下这种方法的使用，具体原理暂时没有深究，有兴趣转Darts,Dice, and coids。

Alias-Method 原理

大部分资料都会以这个例子讲解：游戏中经常遇到按一定的掉落概率来随机掉落指定物品的情况，例如掉落 银币25%，金币20%, 钻石10%，装备5%，饰品40%。现在要求下一个掉落的物品类型，或者说一个掉落的随机序列，要求符合上述概率。

其实方法很简单，最直接的方法就是直接取样，先构建一个累加概率分布列表:[0.25,0.45,0.55, 0.60, 1.0]，之后产生一个随机数(0-1)，假设为0.7，那么在列表中找到第一个大于0.7的数为1.0,对应的类别是第5类。 这种方法很简单直接，但是每次取样复杂度为\(O(K)​\)，使用二分搜索之后，降为\(O(logK)​\)。

论文中经常使用的是另一种很巧妙的方法: Alias Method，它在初始化之后每次随机取样的复杂度为\(O(1)\)。 下面以Darts,Dice, and coids文中例子用图示说明整个步骤，原理太繁杂，不做介绍，参考博客即可:

假设概率分布为: \(\frac{1}{2}, \frac{1}{3}, \frac{1}{12}. \frac{1}{12}\)。

1. 初始概率分布: 类别数目\(K=4\)，以颜色表示不同的类别

2. 每个类别概率乘以K=4,使得总和为4. 这样分为两类，大于1:第一列与第二列; 小于1: 第三列与第四列。

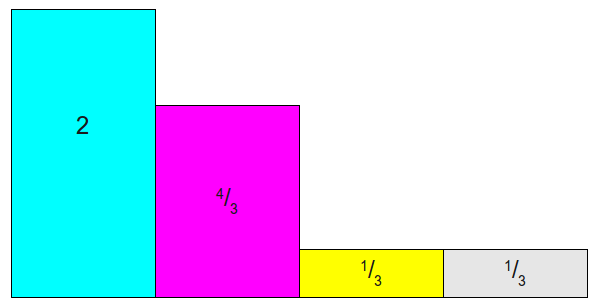
3. 下面通过拼凑，使得每一列的和都为1，但是每一列中，最多只能是两种类型的拼凑，就是每一列最多两种颜色存在。
   • 将第一列拿出\(\frac{2}{3}\)给最后一列，使其变为1，如下:(棕色表示空缺)
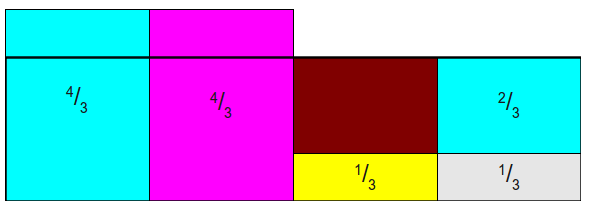
   • 将第一列拿出\(\frac{2}{3}\)给第三列，使之变为1，如下:
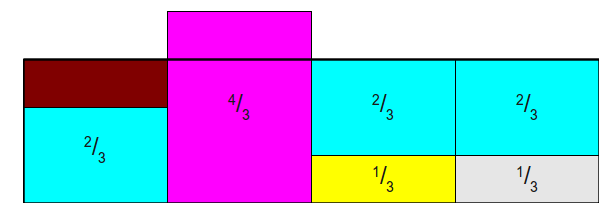
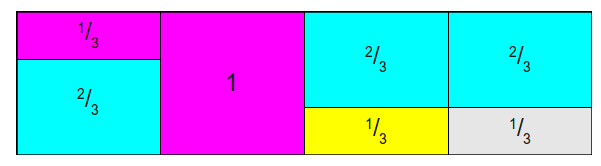
   • 最后一次,第二列给第一列\(\frac{1}{3}\), 最后每一列都是1，且每一列最多两种类型，其中下面一层表示原类的概率，上面层表示另外一种类型的概率，如只有一种比如第二列，那么第二层就是NULL:

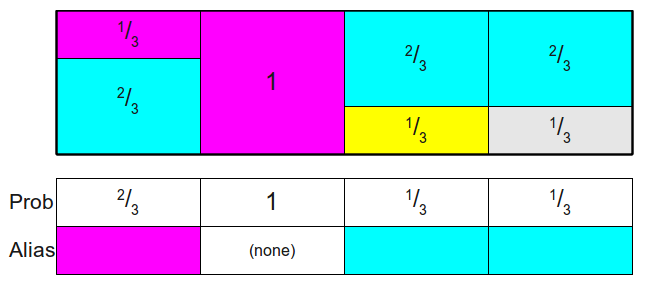
4. 写出两个数组:

   • Probability table \(Prob\): 落在原类型的概率，每一列第一层的概率，即:\([\frac{2}{3}, 1, \frac{1}{3}, \frac{1}{3}]\)
   • Alias table \(Alias\) : 每一列第二层的类型(颜色)，这里用下标表示: \([2, null, 1, ,1]\)

   用图表示如下:

   到此为止，得到\(Prob, Alias\) 表示初始化完成。

5. 采样过程: 随机取某一列k(即[1,4]的随机整数)，再随机产生一个[0-1]的小数c，如果\(Prob[k]\) 大于 c，那么采样结果就是k，反之则为\(Alias[k]\)。

需要说明的是，该过程一定可以结束(原文有证明)。此外在初始化完成之后每次采样的复杂度为\(O(1)\)，因此应用很广。

举个例子说明采样过程，比如随机取得第1列， 随机产生的小数为\(0.5< \frac{2}{3}\)，那么采样的结果就是第一类。 如果随机产生的小数为\(0.8 > \frac{2}{3}\)，那么采样结果就是第一列的第二层的类别，也就是\(Alias[1] = 2\)(紫色对应的类别: 第二列)。

再简单验证下，看看该方法的采样是不是满足原始的概率分布\(\frac{1}{2}, \frac{1}{3}, \frac{1}{12}. \frac{1}{12}\)

对于采到第一种的概率，采到第一种有三部分组成，第一列，第三，四列分别求概率求和: \(\frac{2}{3} * \frac{1}{4} + (1-\frac{1}{3}) * \frac{1}{4} + ({1-\frac{1}{3}}) * \frac{1}{4} = \frac{1}{2}\) ，因此满足原始概率的分布，其余同理。

代码

代码官网给了Java版本，不过网上有很多其他语言的版本，下面参考1 做了注释如下:

import numpy        as np
import numpy.random as npr
 
def alias_setup(probs):
    '''
    probs： 某个概率分布
    返回: Alias数组与Prob数组
    '''
    K       = len(probs)
    q       = np.zeros(K) # 对应Prob数组
    J       = np.zeros(K, dtype=np.int) # 对应Alias数组
    # Sort the data into the outcomes with probabilities
    # that are larger and smaller than 1/K.
    smaller = [] # 存储比1小的列
    larger  = [] # 存储比1大的列
    for kk, prob in enumerate(probs):
        q[kk] = K*prob # 概率
        if q[kk] < 1.0:
            smaller.append(kk)
        else:
            larger.append(kk)
 
    # Loop though and create little binary mixtures that
    # appropriately allocate the larger outcomes over the
    # overall uniform mixture.
    
    # 通过拼凑，将各个类别都凑为1
    while len(smaller) > 0 and len(larger) > 0:
        small = smaller.pop()
        large = larger.pop()
 
        J[small] = large # 填充Alias数组
        q[large] = q[large] - (1.0 - q[small]) # 将大的分到小的上
 
        if q[large] < 1.0:
            smaller.append(large)
        else:
            larger.append(large)
 
    return J, q
 
def alias_draw(J, q):
    '''
    输入: Prob数组和Alias数组
    输出: 一次采样结果
    '''
    K  = len(J)
    # Draw from the overall uniform mixture.
    kk = int(np.floor(npr.rand()*K)) # 随机取一列
 
    # Draw from the binary mixture, either keeping the
    # small one, or choosing the associated larger one.
    if npr.rand() < q[kk]: # 比较
        return kk
    else:
        return J[kk]
 
K = 5
N = 100
 
# Get a random probability vector.
probs = npr.dirichlet(np.ones(K), 1).ravel()
 
# Construct the table.
J, q = alias_setup(probs)
 
# Generate variates.
X = np.zeros(N)
for nn in xrange(N):
    X[nn] = alias_draw(J, q)